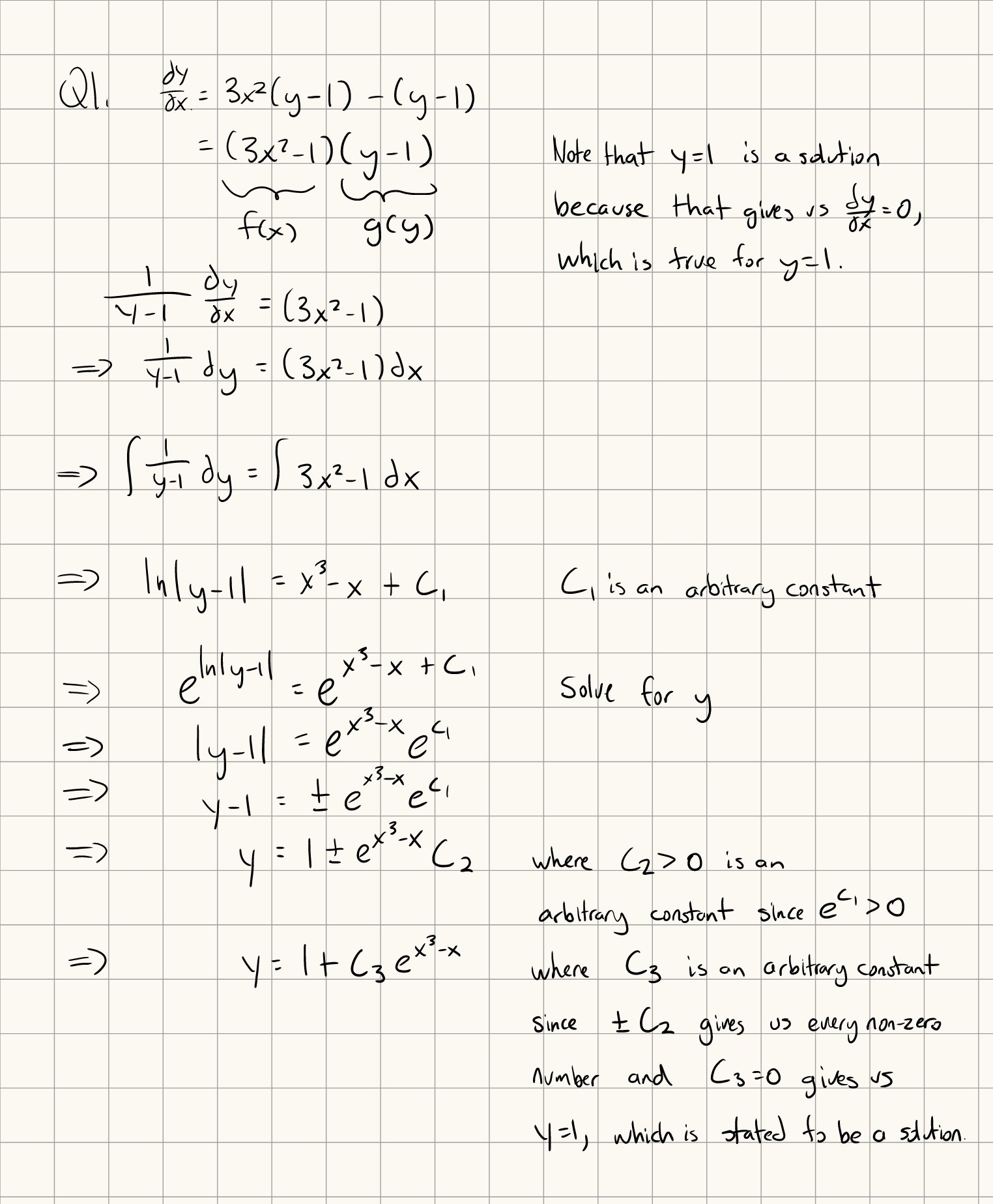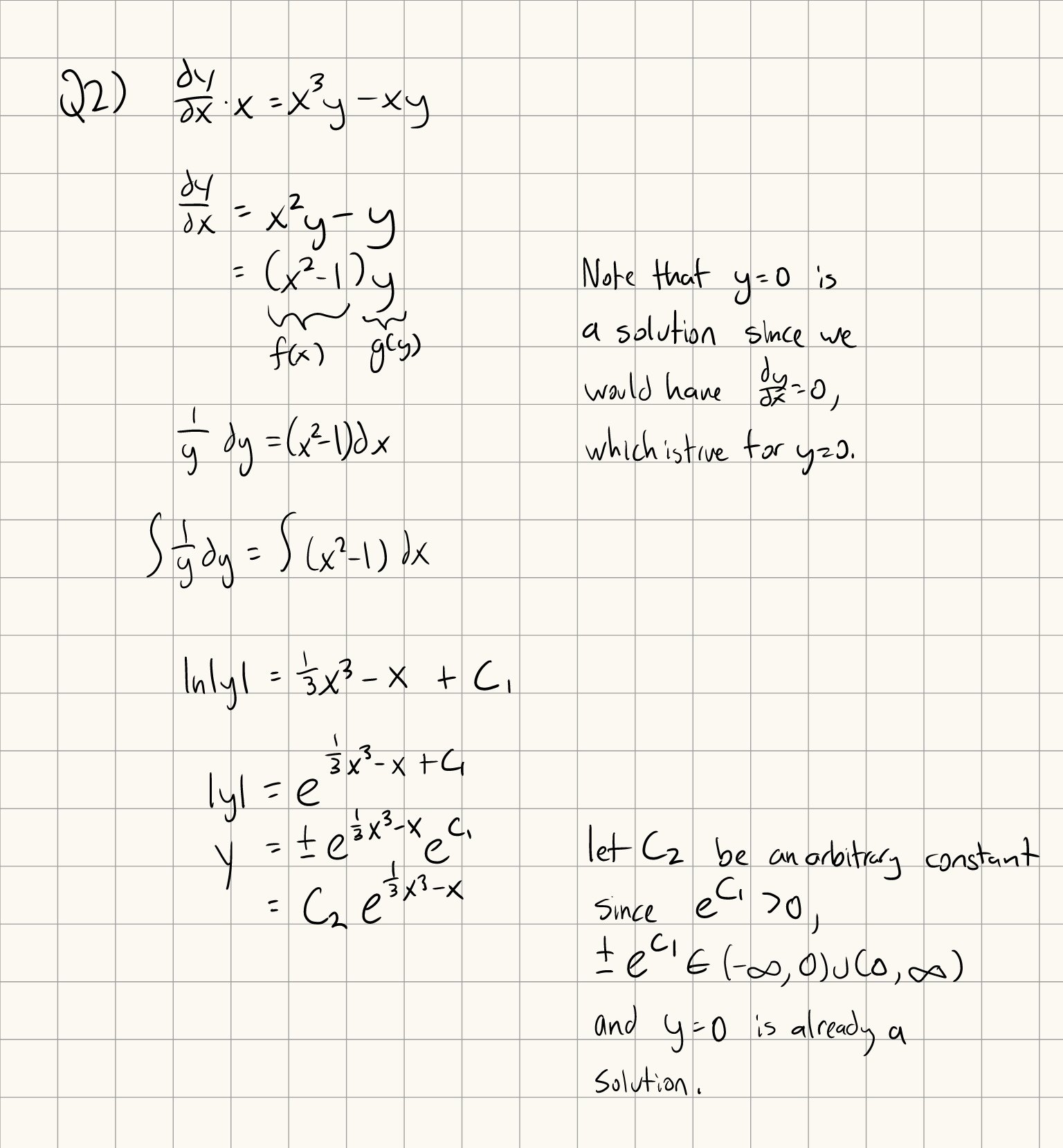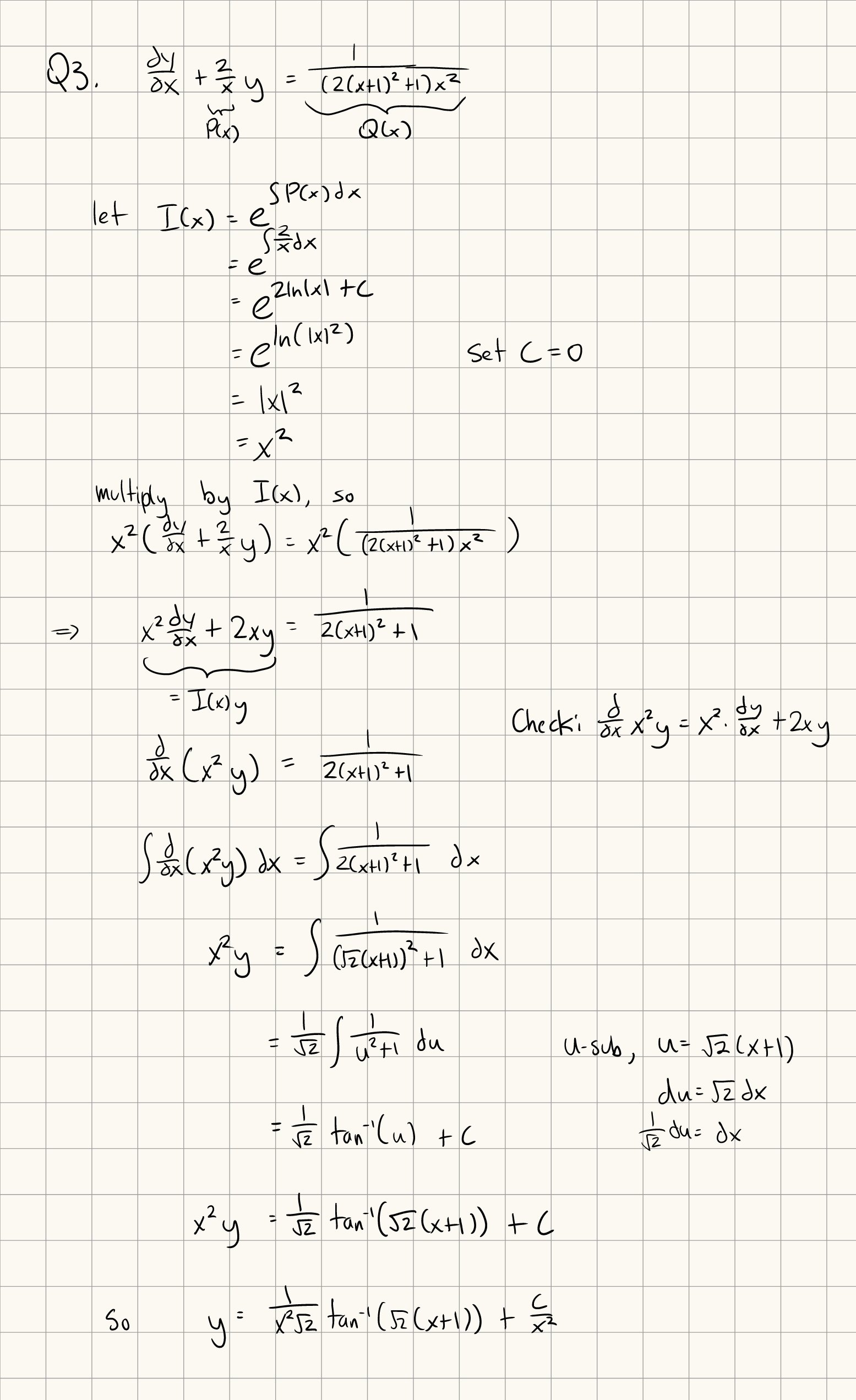Tutorial Week 8

Separable Differential Equations

Separable differential equations are in the form of \(\frac{dy}{dx} = f(x) \cdot g(y)\), where f is a function in terms of x and g is a function in terms of y.

This differential equation can then be rewritten as \(\frac{1}{g(y)} dy = f(x) dx\), and then be integrated on both sides, \(\int \frac{1}{g(y)} dy = \int f(x) dx\).

After computing this integral, you’ll just need to solve for the variable y.

Q1: Solve the differential equation \(\frac{dy}{dx} = 3x^2y - 3x^2 - y + 1\).

Show Solution

Q2: Solve the differential equation \(\frac{dy}{dx}x = x^3y - xy\).

Show Solution

Linear Differential Equations

A first-order linear differential equation the standard form is given by \(\frac{dy}{dx} + P(x)y = Q(x)\).

To solve a first-order linear differential equation, we define the integrating factor as \(I(x) = e^{\int P(x) dx}\), and then multiply both sides of \(\frac{dy}{dx} + P(x)y = Q(x)\) by \(I(x)\) to get \(I(x)(\frac{dy}{dx} + P(x)y) = I(x)(Q(x))\).

With the choice of \(I(x)\), \(I(x)(\frac{dy}{dx} + P(x)y) = I(x)(Q(x))\) simplifies to \(\frac{d}{dx}(I(x)y) = I(x)Q(x)\).

We then integrate both sides (\(\int \frac{d}{dx} (I(x)y) dx = \int I(x)Q(x) dx\)), which simplifies to \(I(x)y = \int I(x)Q(x) dx\), which we can use to solve for y.

Q3: Solve the differential equation \(\frac{dy}{dx} + \frac{2y}{x} = \frac{1}{2x^4 + 4x^3 + 3x^2}\).

Show Solution

Q4: Solve the differential equation \(\frac{dy}{dx} - 4y = e^{2x}\).

Show Solution