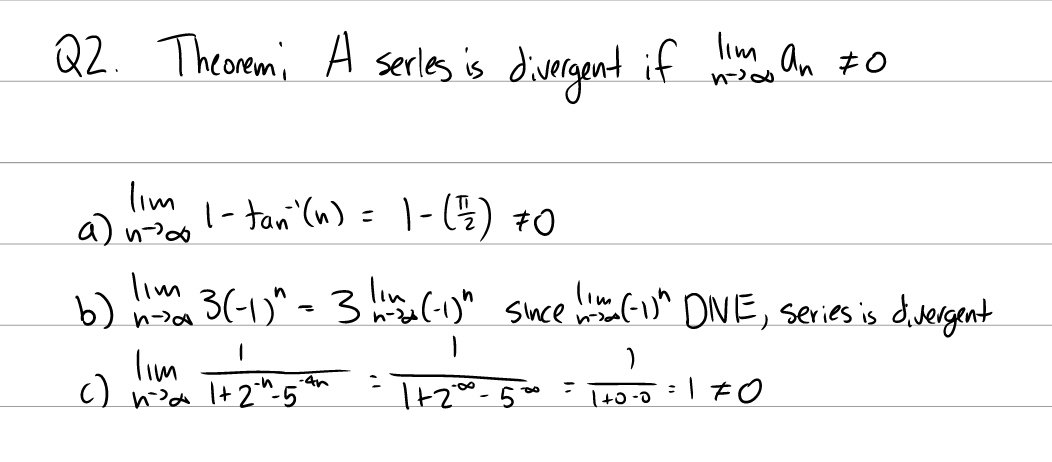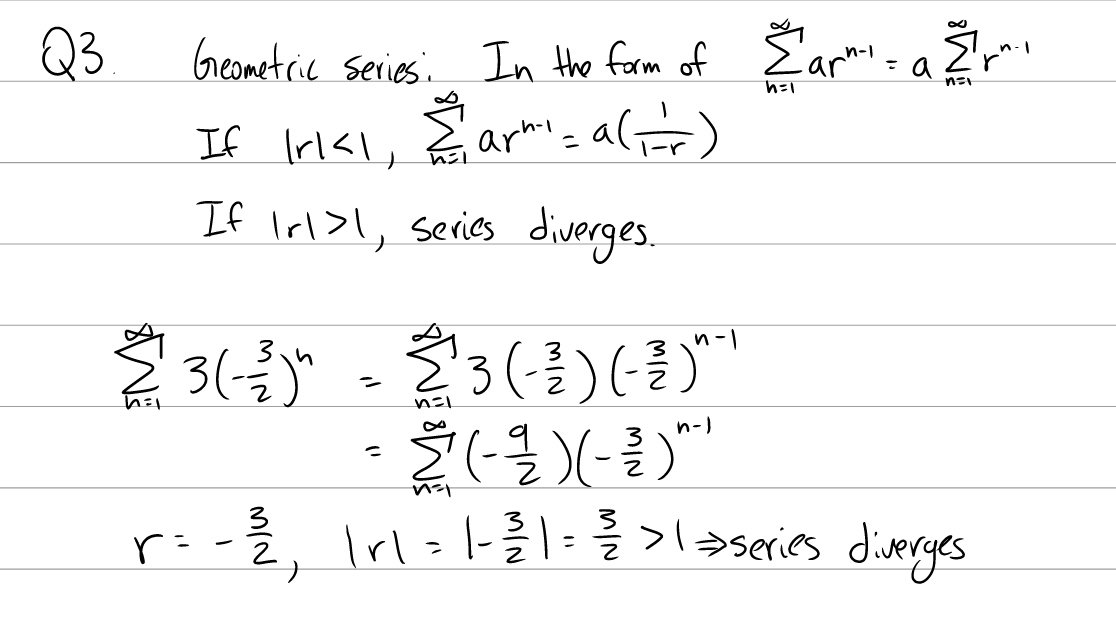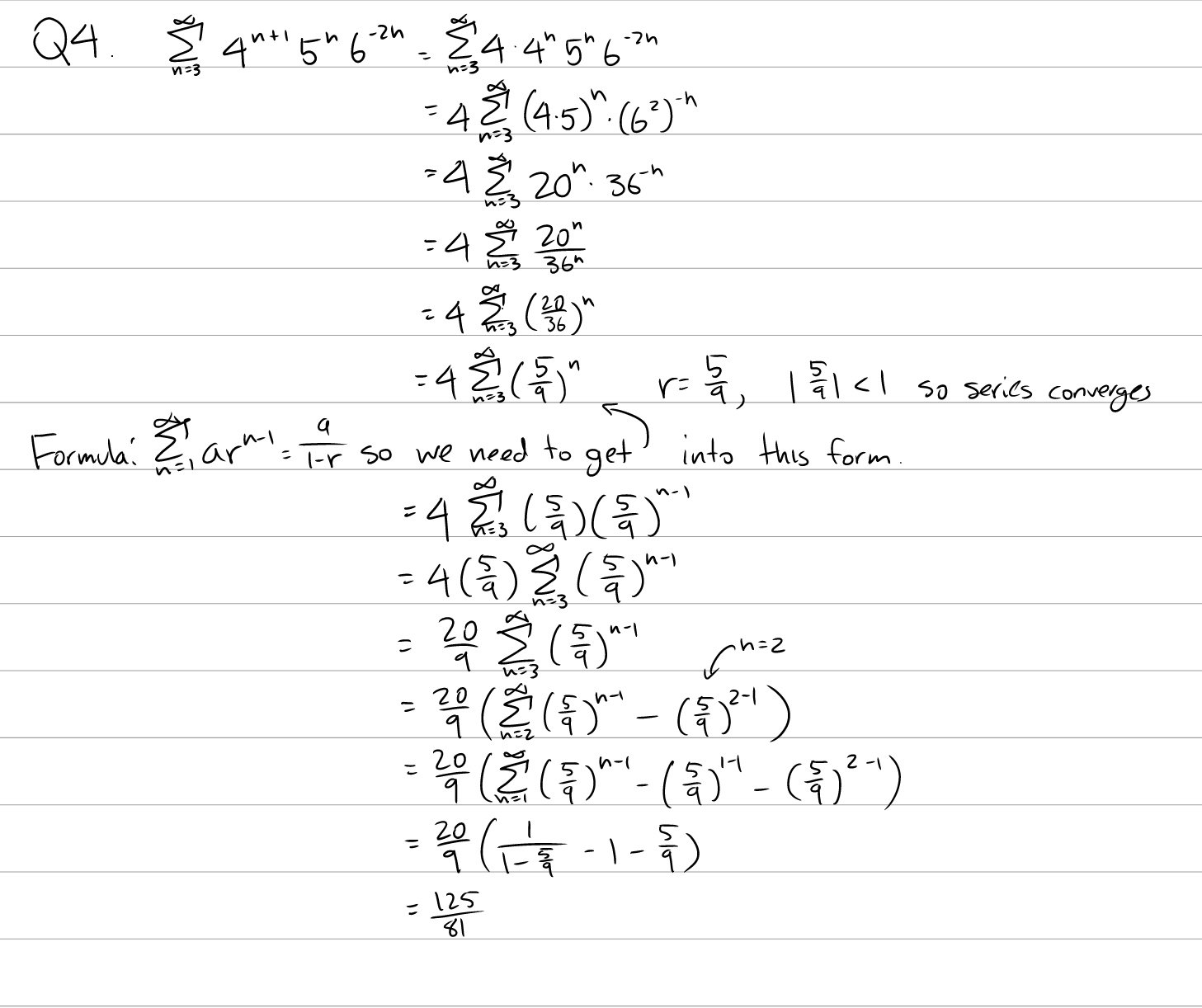Tutorial Week 10
Series Definitions
A series is a sum written in the form \(\sum_{k=1}^\infty a_k\).
A series converges if \(\sum_{k=1}^\infty a_k = L\) for some constant L.
If no such \(L\) exists, then the series diverges.
The divergence test states that if \(\lim_{k \to \infty} a_k \ne 0\), then a series diverges.
Geometric Series
A geometric series is a series in the form of \(\sum_{k=0}^\infty ar^k\).
If \(|r| \lt 1\), then the series converges to \(\frac{a}{1-r}\).
If \(|r| \ge 1\), the series diverges.
Q1: Does \(\sum_1^\infty 1 - \arctan(n)\) converge? If so, find its sum.
Q2: Does \(\sum_{n=1}^\infty 3(-\frac{3}{2})^n\) converge? If so, find its sum.
Q3: Does \(\sum_{n=3}^\infty 4^{n+1}5^n6^{-2n}\) converge? If so, find its sum.
