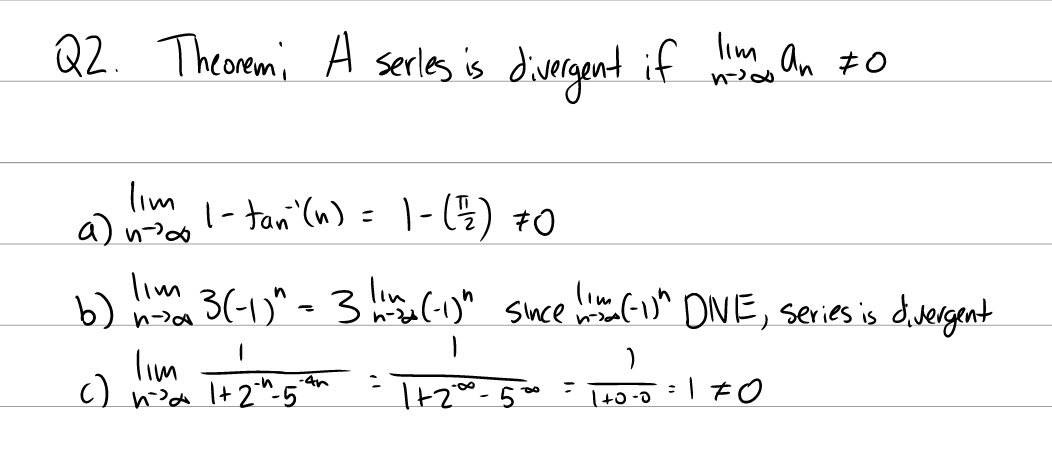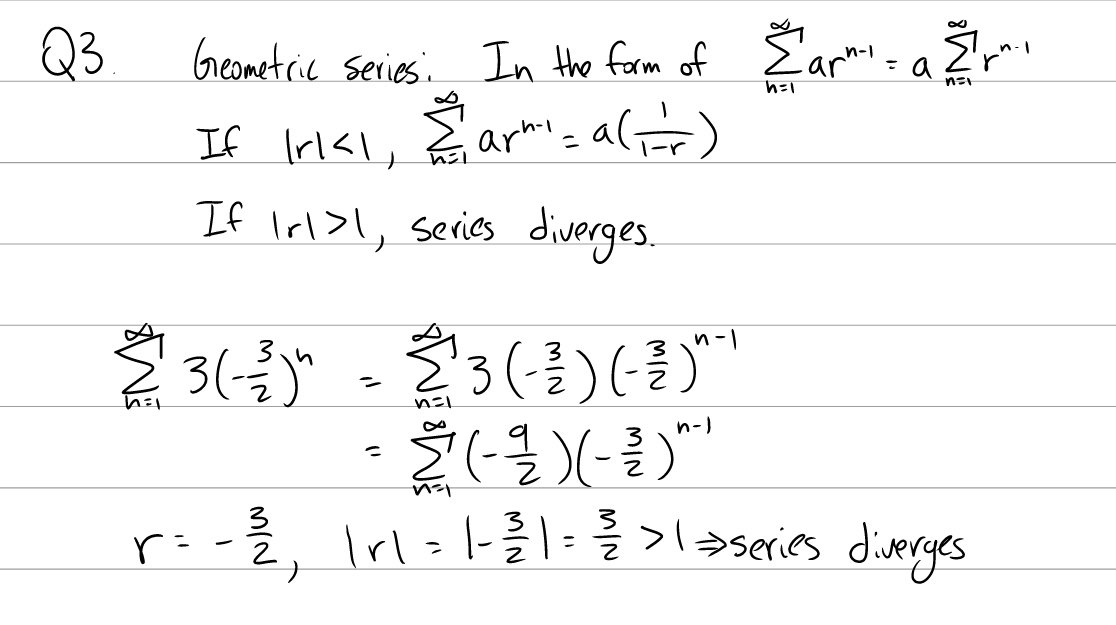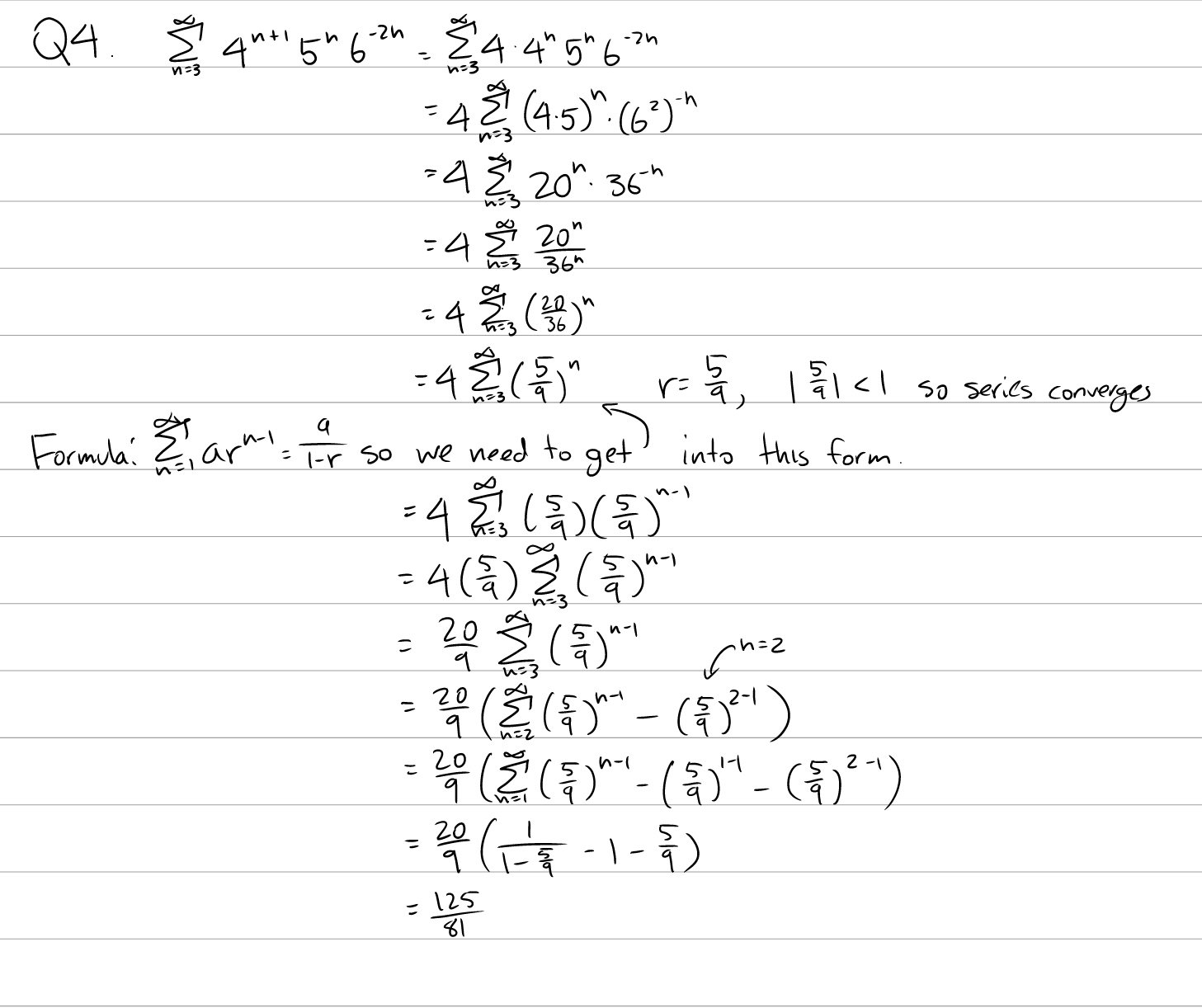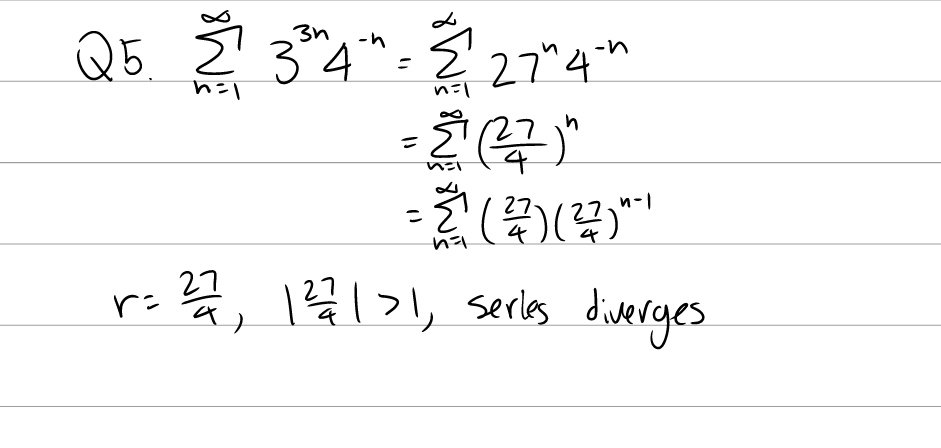Tutorial Week 10
Recursively defined Functions
Q1: Show that the sequence \(a_1 = 1\) \(a_{n+1} = \sqrt{2a_n + 8}\) converges and find the limit it converges to.
Conditions for convergent series
Q2: Show that the following series are divergent.
a. \(\sum_1^\infty 1 - \arctan(n)\)
\(\;\)
b. \(\sum_1^\infty 3(-1)^n\)
\(\;\)
c. \(\sum_1^\infty \frac{1}{1 + 2^{-n} - 5^{-4n}}\)
Geometric Series
Q3: Does \(\sum_{n=1}^\infty 3(-\frac{3}{2})^n\) converge, if so, find its sum.
Q4: Does \(\sum_{n=3}^\infty 4^{n+1}5^n6^{-2n}\) converge? If so, find its sum.
Q5: Does \(\sum_{n=1}^\infty 3^{3n}4^{-n}\) converge? If so, find its sum.
Q6: Does \(\sum_{n=1}^\infty( (\frac{1}{4})^{n-1} - 3(\frac{2^n}{5^{n-2}}))\) converge? If so, find its sum.
