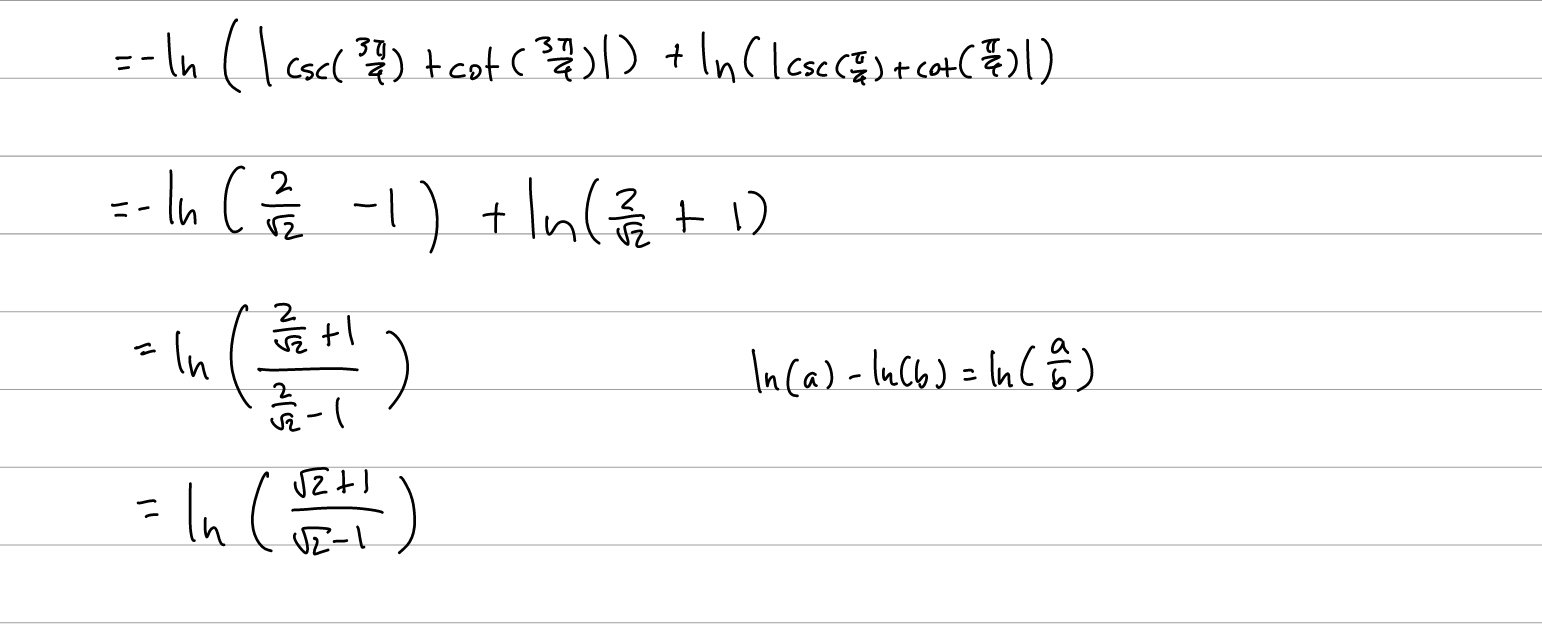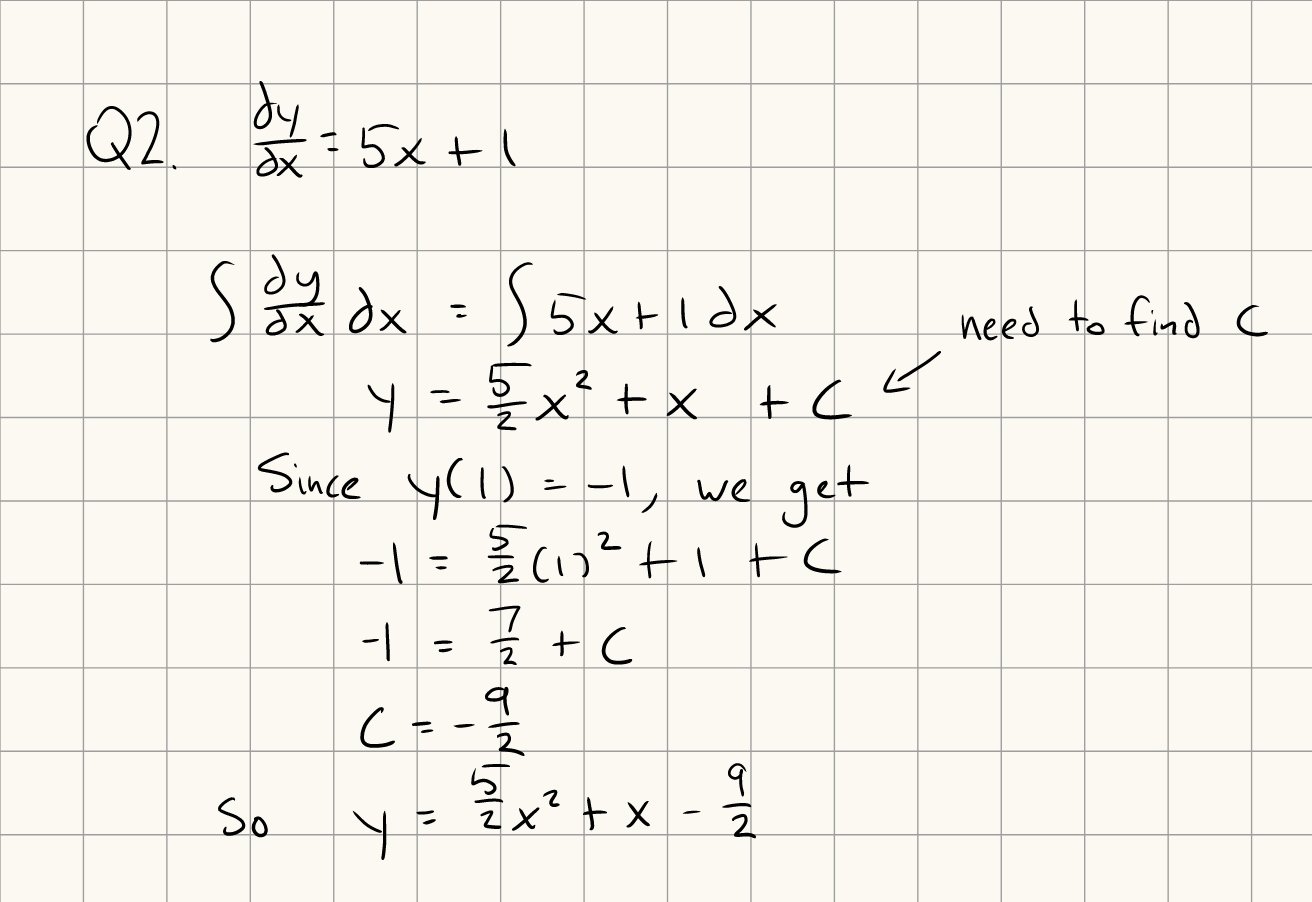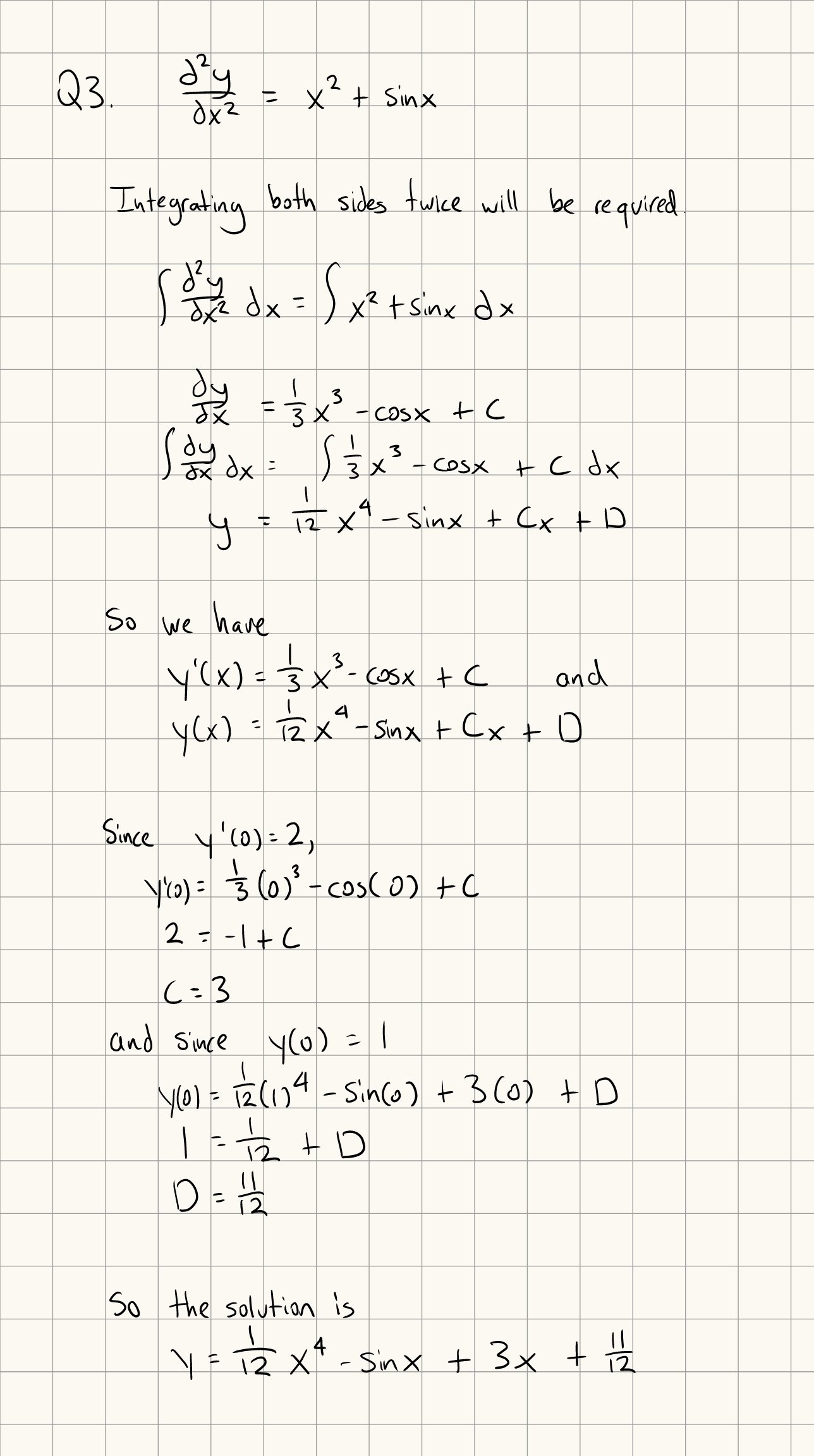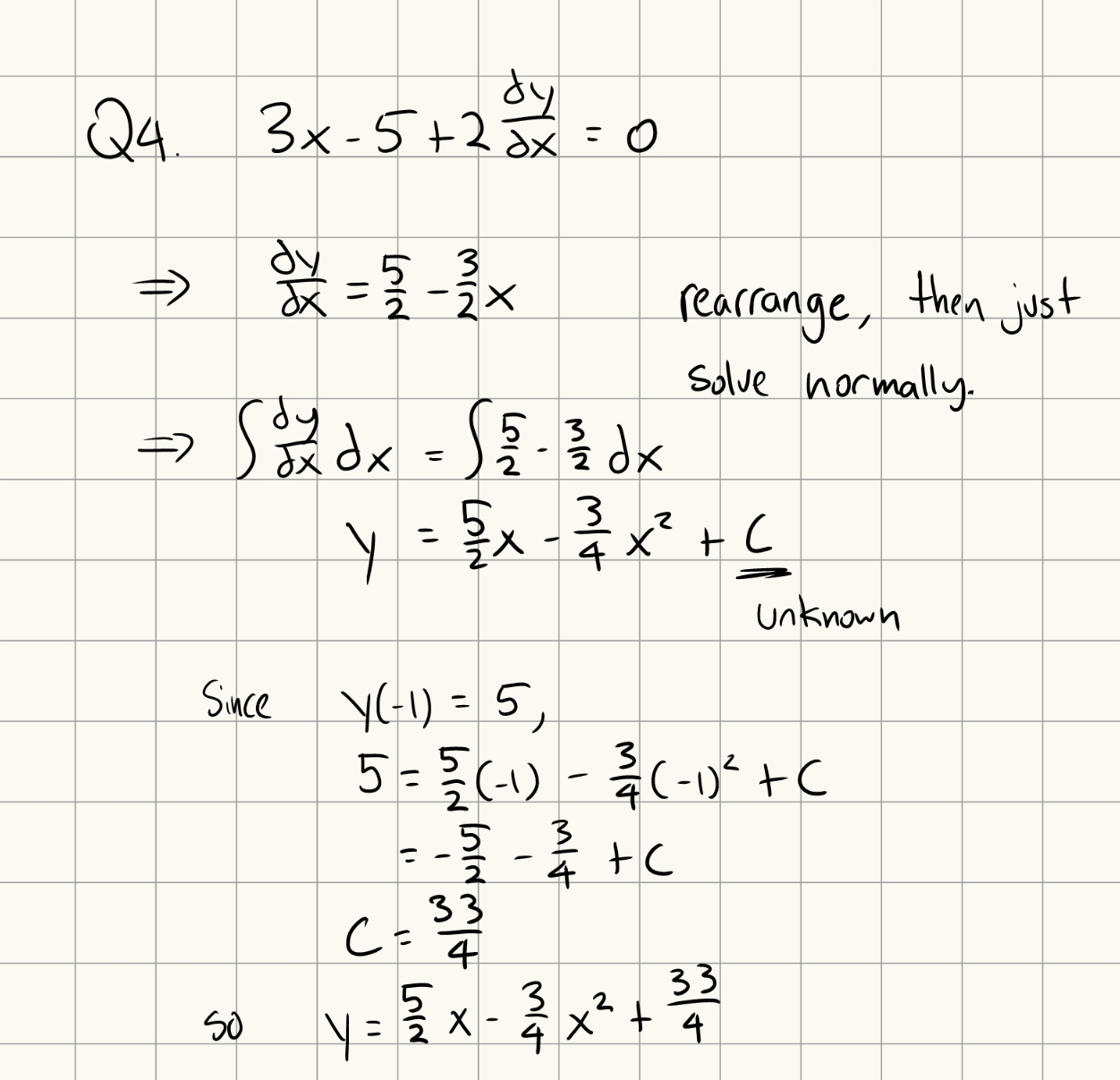Tutorial Week 7
Arc Length
The formula to find the arc length of a function is \(\int_a^b \sqrt{1 + (f'(x))^2} \; dx\).
Q1: Find the length of the curve \(y = -ln(sin(x))\) on \(x \in [\frac{\pi}{4}, \frac{3\pi}{4}]\).
Initial Value Problems (Differential Equations)
Differential equations are equations derivatives of a function, such as \(\frac{dy}{dx} + 2\frac{dy^3}{dx^3} = 1\).
With initial value problems, you’re given a set of initial conditions (i.e. \(y(a) = k\), \(y'(a) = m\)).
Q2: Solve the initial value problem with \(\frac{dy}{dx} = 5x + 1\), with \(y(1) = -1\).
Q3: Solve the initial value problem with \(\frac{d^2y}{dx^2} = x^2 + \sin x\), with \(y(0) = 1\) and \(y'(0) = 2\).
Q4: Solve the initial value problem with \(3x - 5 + 2\frac{dy}{dx}= 0\), with \(y(-1) = 5\).
