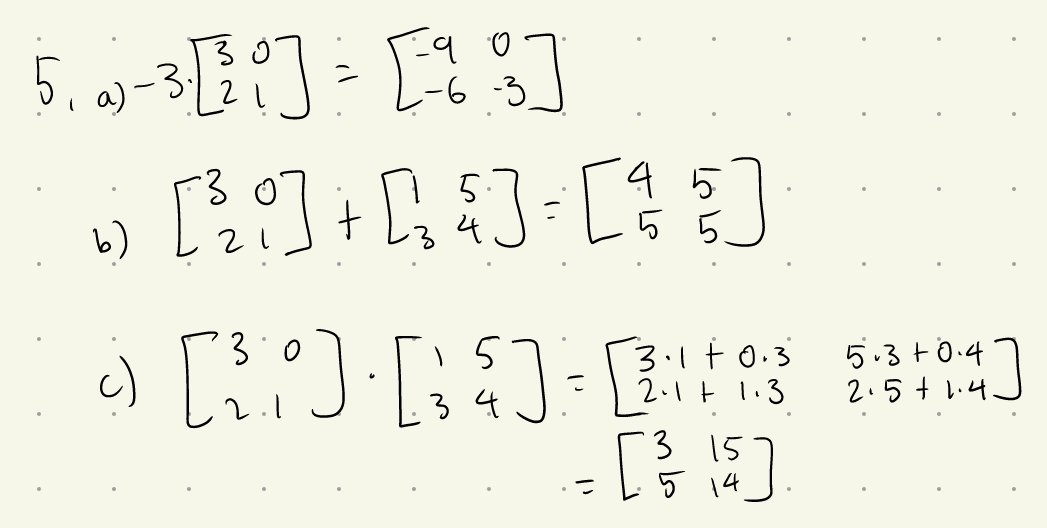Tutorial Week 3
Unbounded Regions
Q1: Find the minimal value of \(Z =x+3y\) given the constraints \(\begin{cases} 2x+4y\ge6 \\ 5x+y\ge5 \\ x, y \ge 0 \end{cases}\).
Q2: Is there a maximal value for the above function \(Z\)?
Numbers of Solutions
Q3: For the above question, if \(Z = x + 2y\), how many solutions would there be?
Matrices
Q4: Evaluate the following.
\(-3 \cdot \begin{bmatrix} 3 & 0 \\ 2 & 1 \end{bmatrix}\)
\(\rule{0pt}{4ex}\) 2. \(\begin{bmatrix} 3 & 0 \\ 2 & 1 \end{bmatrix} + \begin{bmatrix} 1 & 5 \\ 3 & 4 \end{bmatrix}\)
\(\rule{0pt}{4ex}\) 3. \(\begin{bmatrix} 3 & 0 \\ 2 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 5 \\ 3 & 4 \end{bmatrix}\)?
Q5: Find all diagonal matrices C such that \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = C^2 + \begin{bmatrix} -1 & 2 \\ 3 & 1 \end{bmatrix}\).
Q6: Represent \(\begin{cases} 3x^3 + 7x^2 - x + 1 = 0 \\ 6x^2 + 5x = 0 \\ 12x^3 - x^2 + 9x + 1 = 0 \end{cases}\) as a matrix. Write this in the form of \(AX = B\), where \(A\) is the coefficient matrix, \(X\) is the variable matrix, and \(B\) is the solution matrix.
