Tutorial Week 2
Welcome to your first tutorial! This tutorial will be about linear inequalities and linear programming.
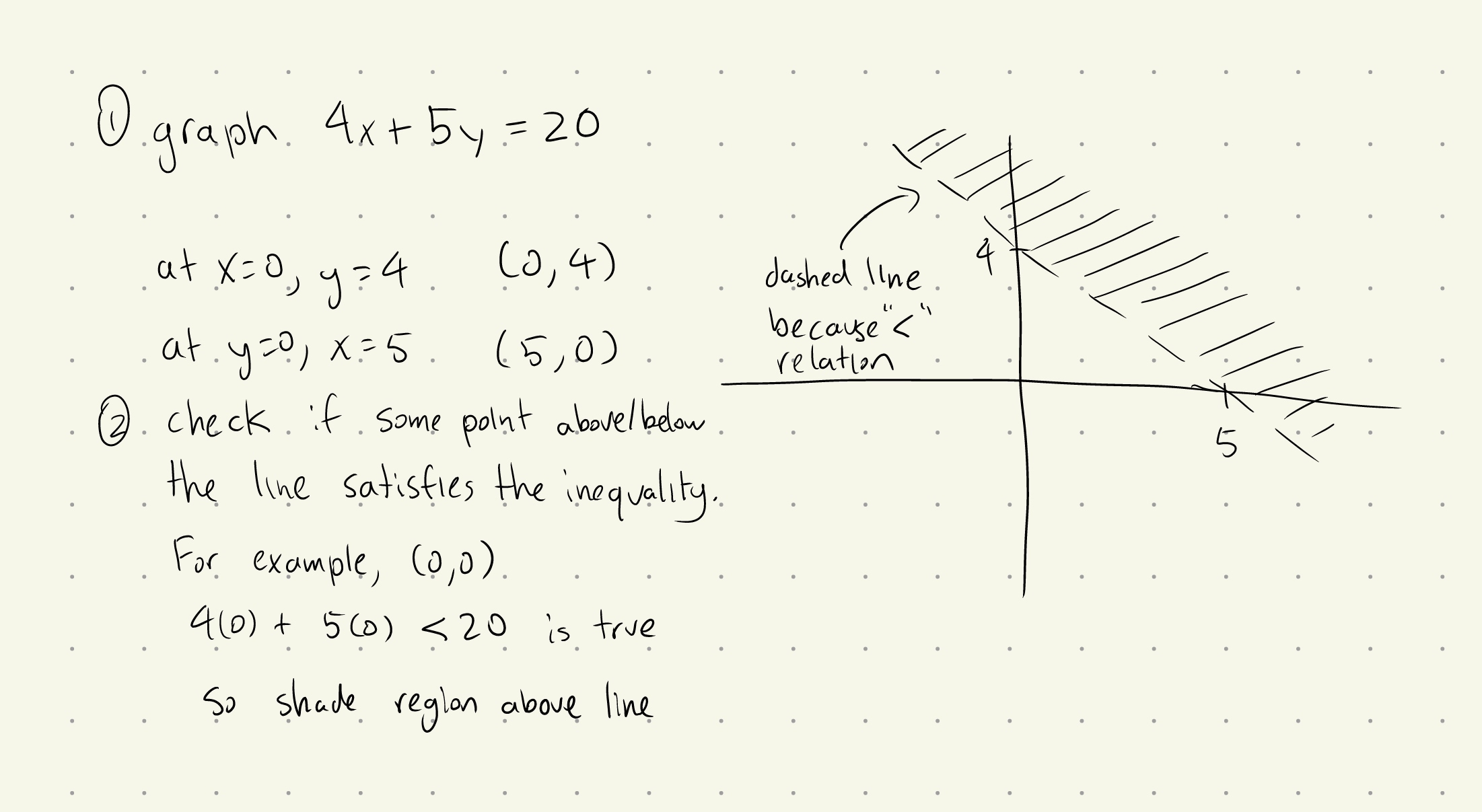
Graphing Linear Inequalities
Q1: Find the solutions for \(4x + 5y \lt 20\).
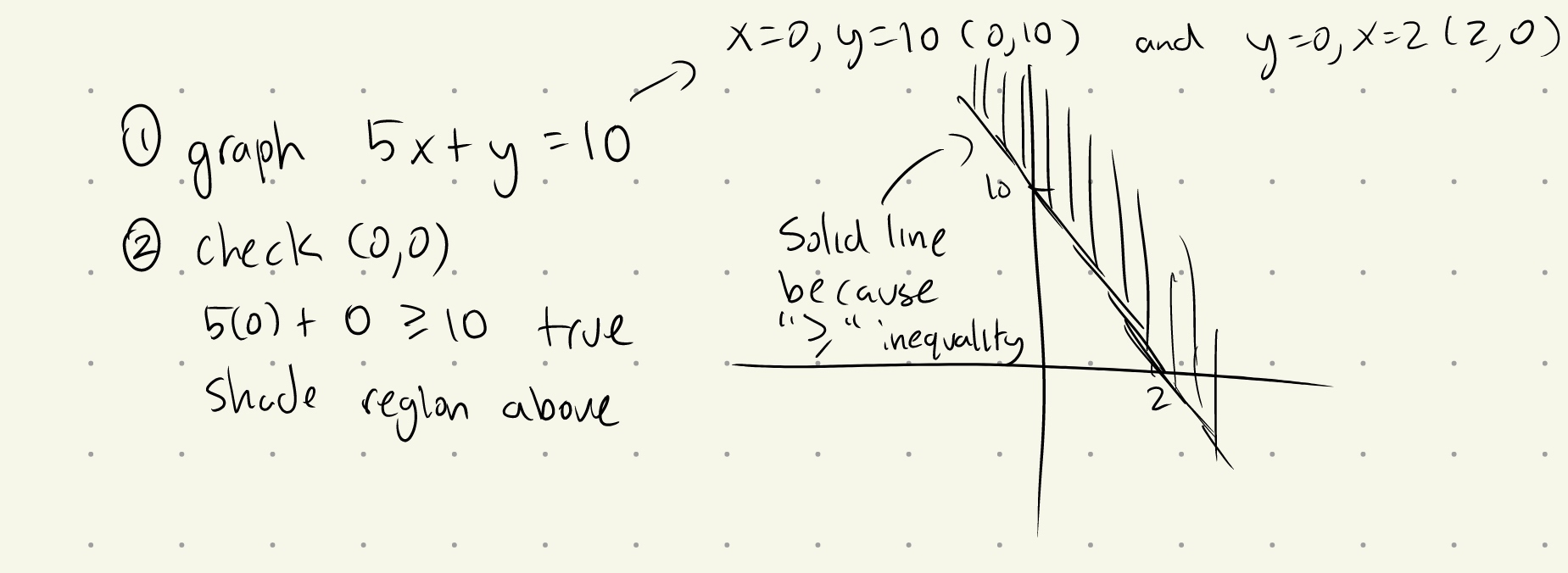
Q2: Find the solutions for \(5x + y \geq 10\).
Q3: Find the solutions for \(\begin{cases} x+y\le6 \\ 3x-y\le9 \\ 2x\ge1 \end{cases}\).
Q4: Find the solutions for \(\begin{cases} 2x-y>-2 \\ y\ge1 \\ x+y=3 \end{cases}\).
FTLP and Feasable regions
Fundamental theorem of Linear Programming:
A linear function (of the form \(f(x) = ax + by\)) has a maximum and minimum at one of its corner points if it is defined on a feasible region that is
non-empty (contains at least one point)
bounded (does not extend to infinity in any direction)
standard (e.g. bounded by \(\leq\) rather than \(\lt\) so that all edges and corners are in the region)
Q5: Do the following regions satisfy the conditions of the Fundamental theorem of Linear Programming?
a)
b)
Finding optimal solutions to Linear Programming problems
Q6: Suppose a school lunch program serves two types of food: A and B. Food A requires 4 minutes and $10 to prepare and food B requires 6 minutes and $5 to prepare. The lunch program has a budget of $200 and two hours to prepare the food. How could you maximize the amount of food items prepared?
Q7: A feasible region is defined by \(\begin{cases} 6x+2y\le12 \\ x-y\ge0 \\ x,y \geq 0 \end{cases}\). What values of \(x, y\) maximize \(Z = x+2y\)?
Related: https://www.youtube.com/watch?v=hNqLAwyhT-4&list=PLD3fYc0bAjC-Wc4icC2F34Bry3oLpFb8B&index=7