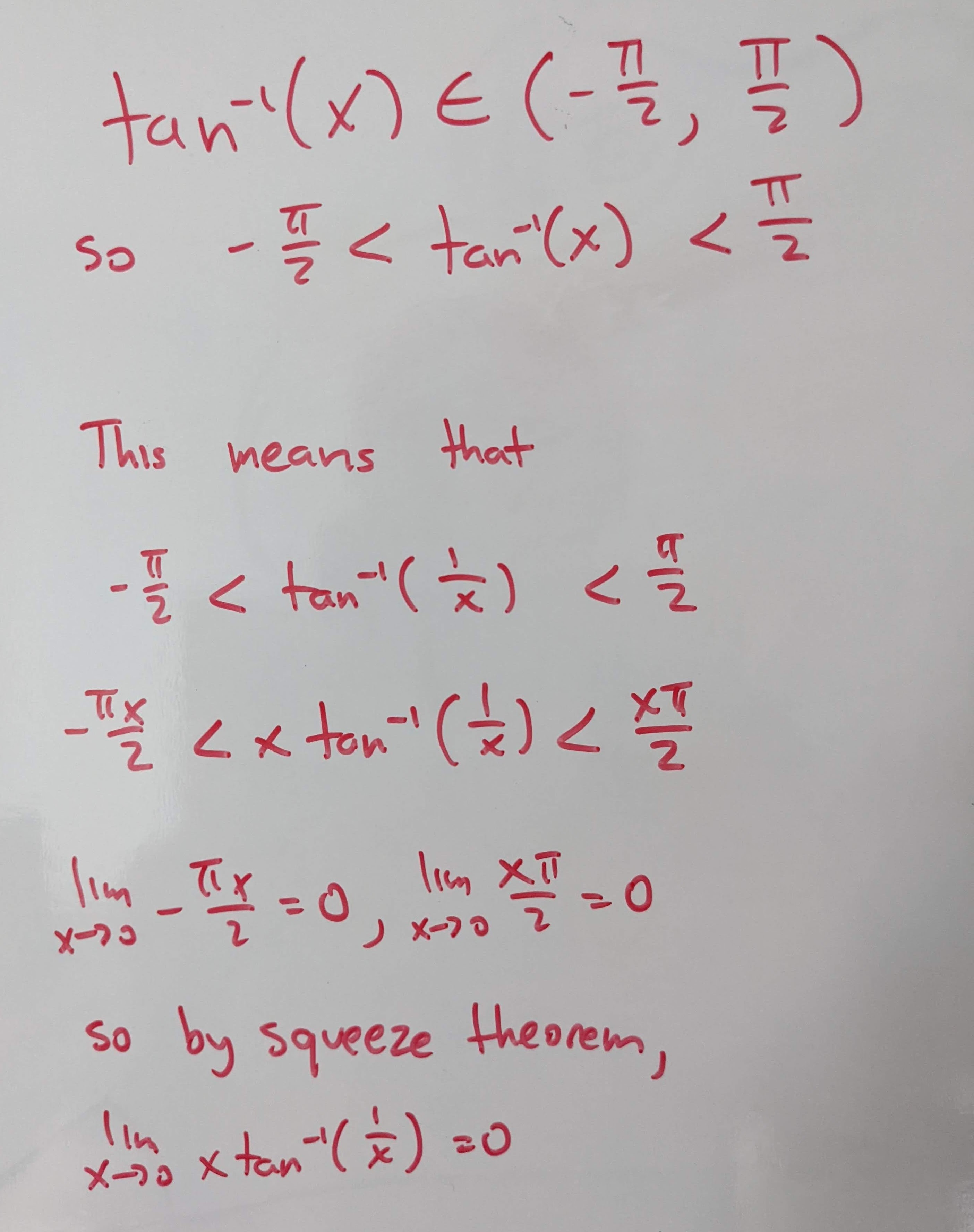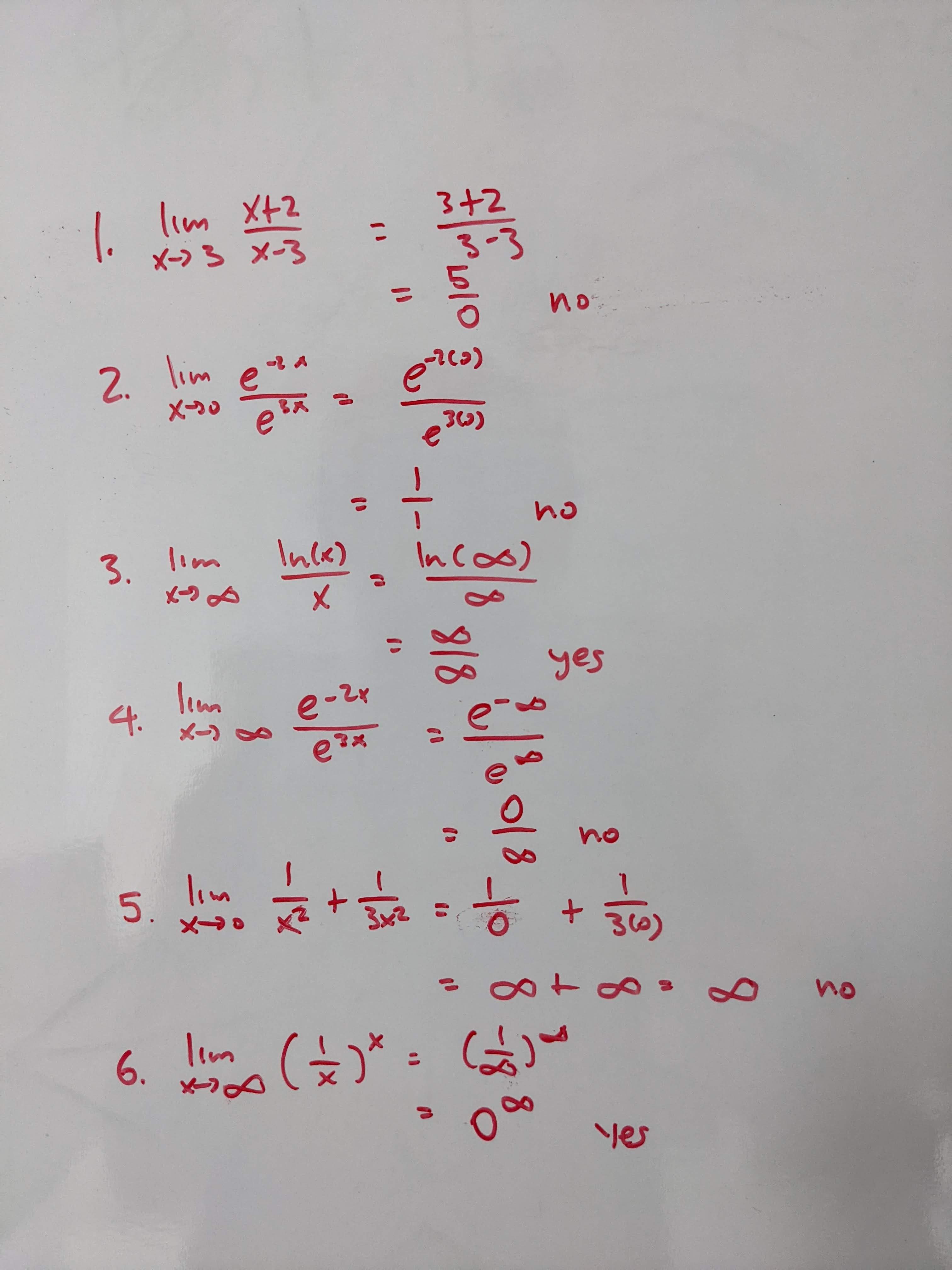Tutorial Week 4

In this tutorial, we’ll be mainly focusing on limits and the different ways to find limits.

Proof of Trigonometric Limit Identities

Prove why \(\lim_{x \to 0} \frac{\sin(x)}{x} = 1\).

Squeeze Theorem

Q1: What is \(\lim_{x \to 0}\; xtan^{-1}(\dfrac{1}{x})\)?

Show Solution

Q2: Calculate \(lim_{x \to \infty} \; \dfrac{3x^2 + \sin(x^3)}{4x^2 - 2}\).

Show Solution

Indeterminant Forms

Q3: Do the following lead to interdeterminate forms?

1. \(\lim_{x \to 3} \frac{x + 2}{x - 3}\)

2. \(\lim_{x \to 0} \frac{e^{-2x}}{e^{3x}}\)

3. \(\lim_{x \to \infty} \frac{ln(x)}{x}\)

4. \(\lim_{x \to \infty} \frac{e^{-2x}}{e^{3x}}\)

5. \(\lim_{x \to 0} \frac{1}{x^2} + \dfrac{1}{3x^2}\)

6. \(\lim_{x \to \infty} (\frac{1}{x})^{x}\)

Show Solution

Conjugates

Q4: Find the limit \(\lim_{x \to 9} \frac{3 - \sqrt{x}}{9x - x^2}\).

Show Solution

Finding Limits

Q5: Let \(f(x) = \begin{cases} x < 1 & x^3 + xk \\ x > 1& \frac{1 + x^2k}{xk}\end{cases}\). For what values of \(k\) does \(\lim_{x \to 1} f(x)\) exist?

Show Solution

Q6: Compute \(\lim_{x \to -1} \frac{x + 1}{|x + 1|}\) if it exists.

Show Solution

Q7: Compute \(\lim_{x \to -1} \frac{7 - |x|}{x^3 + 2}\) if it exists.

Show Solution

Q8: Compute \(\lim_{x \to \infty} \frac{\sqrt{2x^2 + 1}}{3x - 5}\).

Show Solution

Q9: Compute \(\lim_{x \to \infty} 3x - \sqrt{9x^2 - 1}\).

Show Solution

Q10: Compute the horizontal asympotote of \(f(x) = x - \sqrt{2x^2 + 3x + 2}\).

Show Solution

Trigonometric Limits

Q11: Does the limit \(\lim_{x \to 0} sin(\frac{1}{x})\) exist?

Show Solution

Q12: Given an arbitrary constant \(k\), what is \(lim_{x \to 0}\; \cot(2kx)2kx + k\)?

Show Solution

Q13: Compute \(\lim_{x \to 0} \frac{\sin(e\cos(x))}{x}\) if it exists.

Show Solution