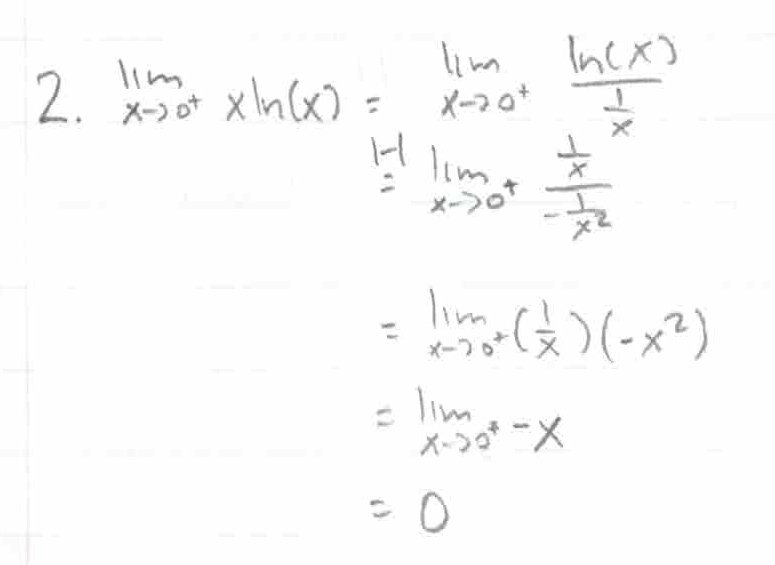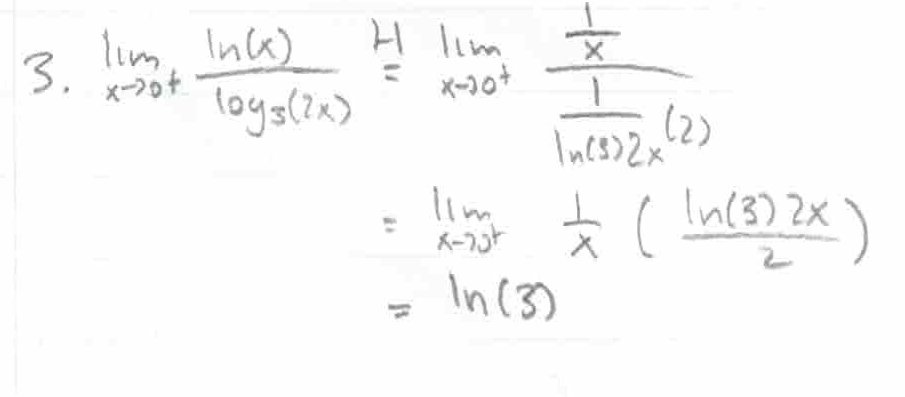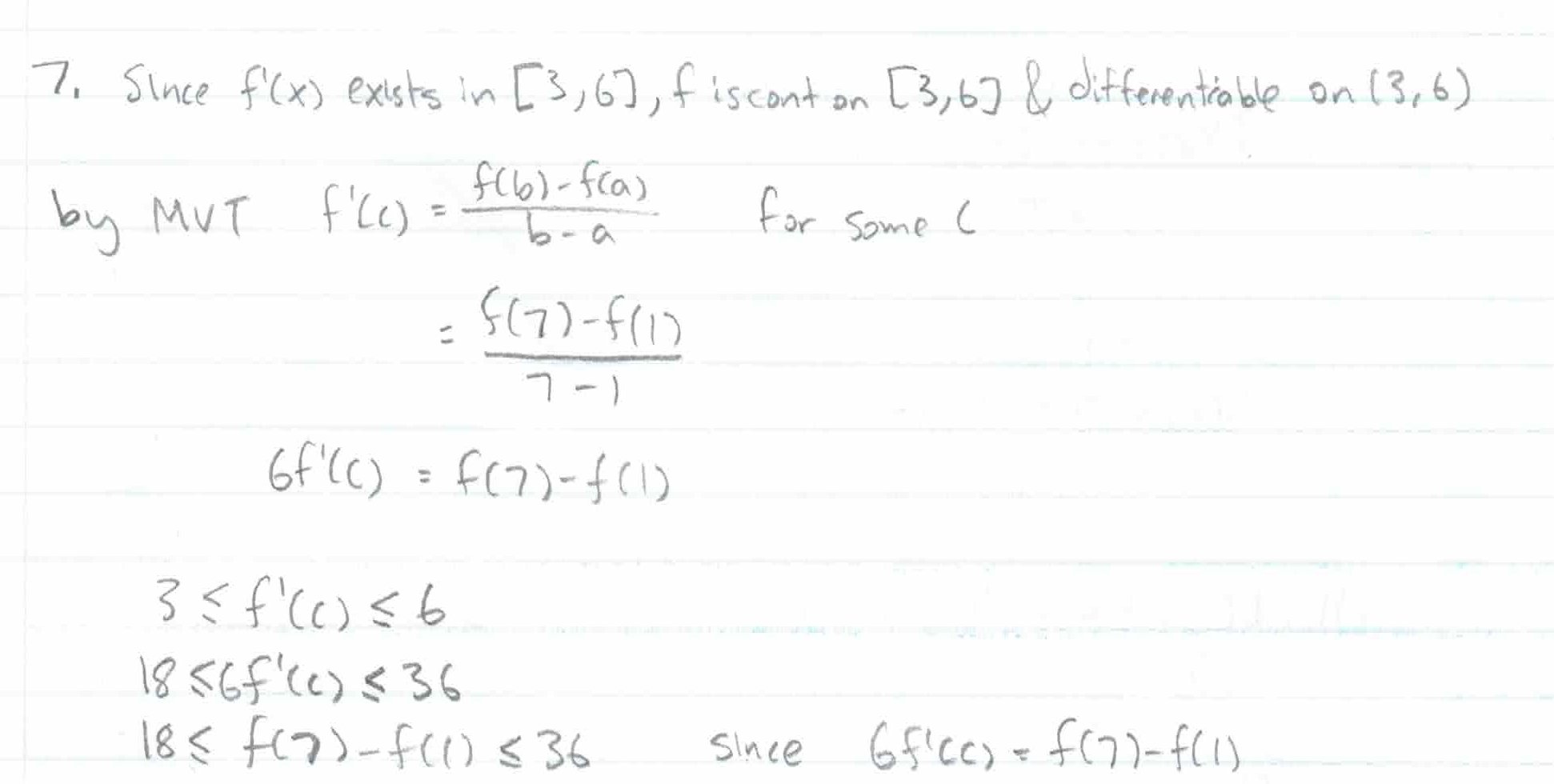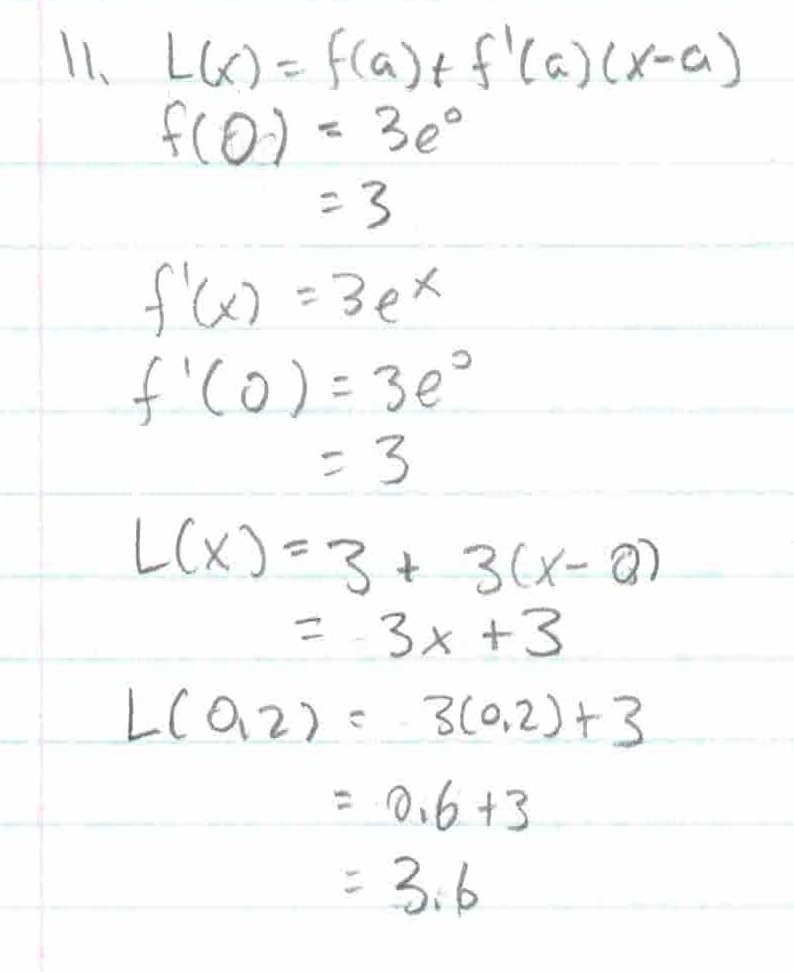Tutorial Week 9

L’Hopital’s Rule

L’Hopital’s rule provides an easy to solve limits that otherwise would have been impossible/very difficult to compute using conventional algebra.

To use L’Hoptial’s rule, the limit must be in an indeterminate form. These are:

• \(\frac{0}{0}\)

• \(\frac{\infty}{\infty}\)

• \(\infty - \infty\)

• \(0^0\)

• \(1^\infty\)

• \(\infty^0\)

• \(0 \cdot \infty\)

Q1: Find \(\lim_{x \to 0} \frac{x + sin(x)}{x^2 + cos(x)sin(x)}\).

Show Solution

Q2: Find \(\lim_{x \to 0^+} xln(x)\).

Show Solution

Q3: Find \(\lim_{x \to \infty} \left(\frac{1}{e^{x}}+1\right)^{e^{x}}\).

Show Solution

Mean Value Theorem

The Mean Value Theorem (MVT) states that:

If a function f is continuous on \([a, b]\) and differentiable on \((a, b)\), then there exists a \(c \in (a, b)\) such that \(f'(c) = \frac{f(b) - f(a)}{b - a}\).

Q4: If \(3 \leq f'(x) \leq 6\) for all \(x\), show that \(18 \leq f(7) − f(1) \leq 36\).

Show Solution

Linearization

Linearization is a computationally simple method of getting a good approximation of the value of a function near some point.

The linearization of a function f at a point a is given by the formula: \(L(x) = f(a) + f'(a)(x-a)\). Essentially, this is an approximation of f near f(a).

Q5: Find the linear approximation of \(f(x) = 3e^{x}\) at \(x=0\). Use it to approximate \(3e^{0.2}\).

Show Solution