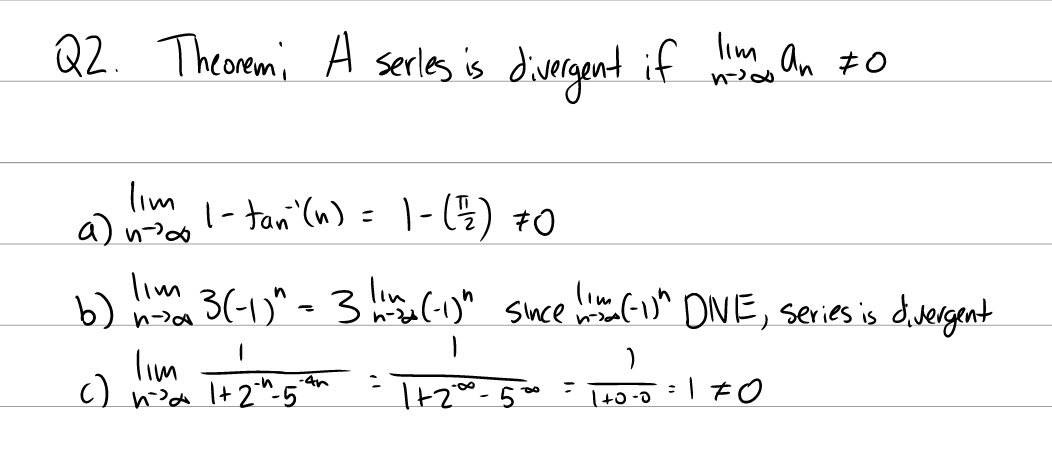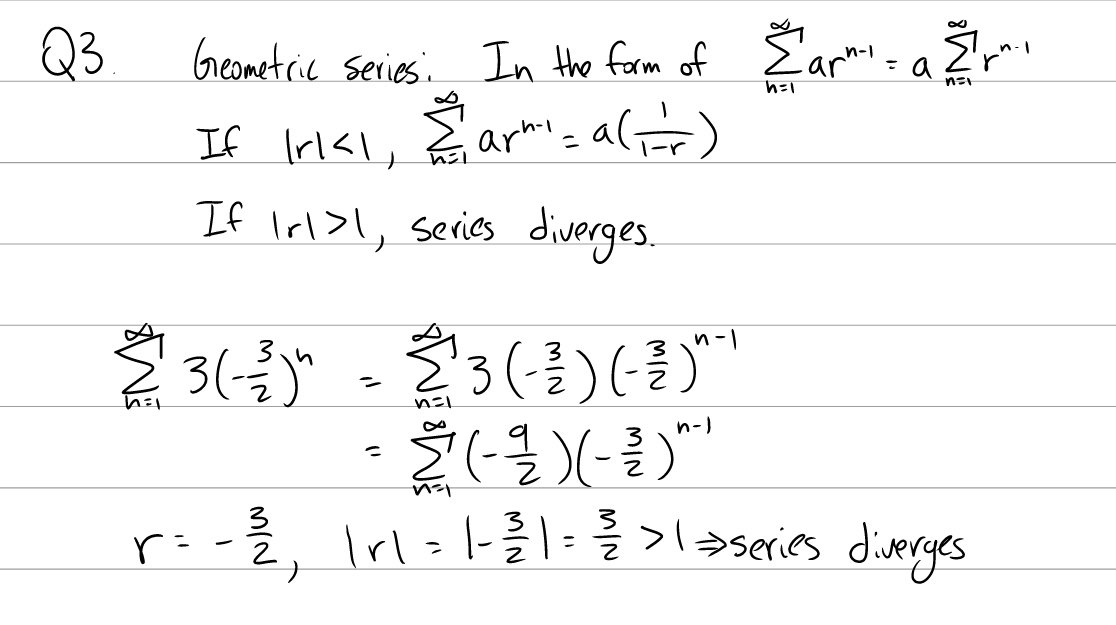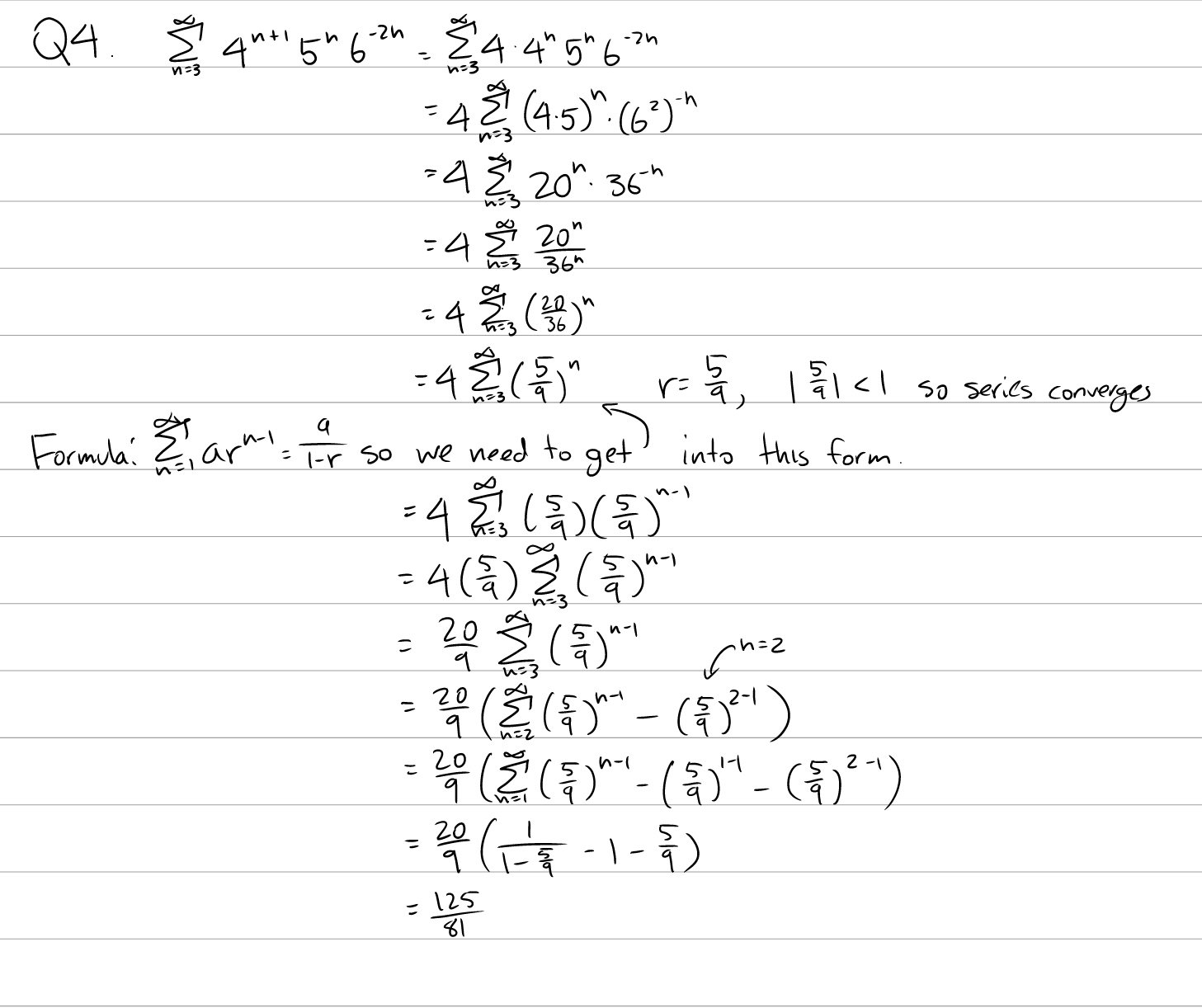Tutorial Week 11

Series Definitions

A series is a sum written in the form \(\sum_{k=1}^\infty a_k\).

A series converges if \(\sum_{k=1}^\infty a_k = L\) for some constant L.

If no such \(L\) exists, then the series diverges.

The divergence test states that if \(\lim_{k \to \infty} a_k \ne 0\), then a series diverges.

Geometric Series

A geometric series is a series in the form of \(\sum_{k=0}^\infty ar^k\).

If \(|r| \lt 1\), then the series converges to \(\frac{a}{1-r}\).

If \(|r| \ge 1\), the series diverges.

Q1: Does \(\sum_1^\infty 1 - \arctan(n)\) converge? If so, find its sum.

Show Solution

Q2: Does \(\sum_{n=1}^\infty 3(-\frac{3}{2})^n\) converge? If so, find its sum.

Show Solution

Q3: Does \(\sum_{n=3}^\infty 4^{n+1}5^n6^{-2n}\) converge? If so, find its sum.

Show Solution

Comparison Test

The comparison test states:

Given series \(\sum a_n\) and \(\sum b_n\), where \(a_n \ge 0\) and \(b_n \ge 0\),

1. If \(\sum a_n\) converges and \(b_n \le a_n\), then \(\sum b_n\) converges.

2. If \(\sum a_n\) diverges and \(a_n \le b_n\), then \(\sum b_n\) diverges.

Q4: Use the comparison test to show whether \(\sum_{n=1}^\infty \frac{3n + 5}{2^n + 5^n - 1}\) converges.

Show Solution

Alternating Series Test

The alternating series test states:

Given an alternating series in the form of \(\sum (-1)^n b_n\) where \(b_n \gt 0\), if \(b_n\) forms a decreasing sequence (\(b_{n+1} \le b_n\)) and \(\lim_{n \to \infty} b_n = 0\), then \(\sum (-1)^n b_n\) converges.

Q5: Does the series \(\sum_{n=1}^\infty \frac{(-1)^nn^2}{n^2+n}\) converge? If it converges, is it absolutely or conditionally convergent?

Show Solution

Q6: Does the series \(\sum_{n=1}^\infty \frac{(-1)^nn}{n^2+n}\) converge? If it converges, is it absolutely or conditionally convergent?

Show Solution