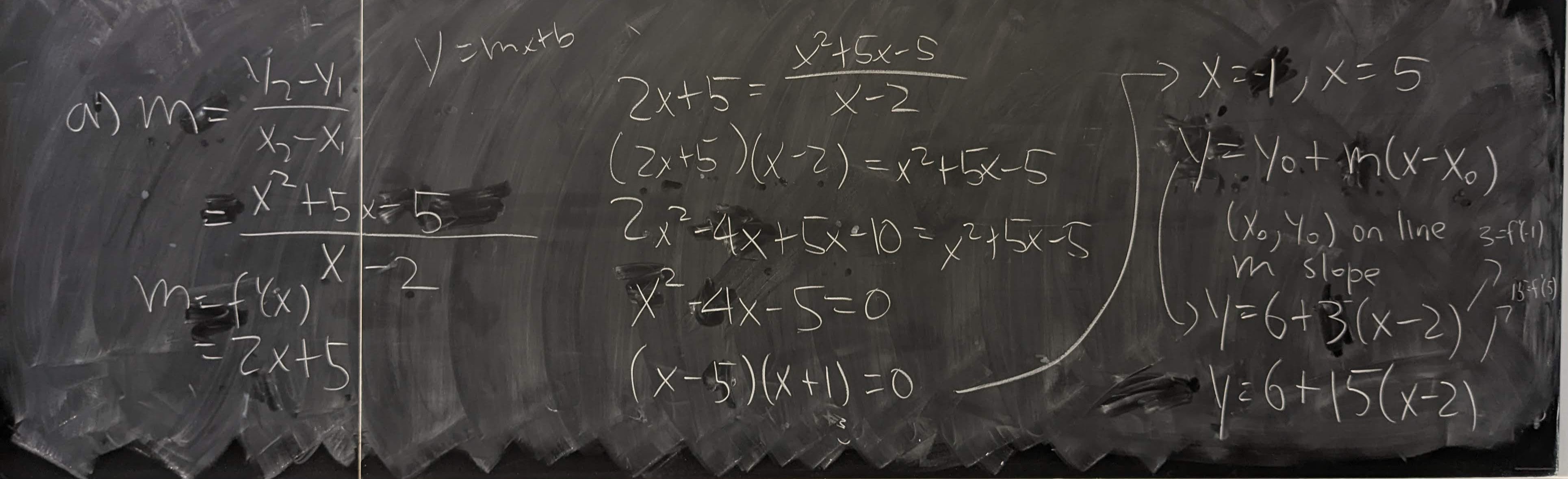Tutorial Week 11

This week, we’ll be preparing for your term test on Friday.

Definitions

You should know the definitions for the following:

• Intermediate Value Theorem

• Extreme Value Theorem

• Critical Point

• Inflection Point

• Continuity at a point

• Limit definition of a derivative

Intermediate Value Theorem

Recall that the intermediate value theorem (IVT) states that if a function f(x) is continuous on the interval [a, b], and \(\forall n\) between f(a) and f(b), \(\exists c \in [a, b]\) such that \(f(c) = n\).

You should know how to apply the IVT, and how do find the values of variables that make a function continuous.

Q1: Show that \(e^{2x} + 2x^2 - 4\) has a root between 0 and 1.

Show Solution

Limit Definition of a Derivative

You should know how to apply the limit definition of a deriviative to compute them.

One key thing to remember here is to multiply by the conjugate when you encounter square roots that can’t be easily simplified.

Computing Deriviatives

There are a few things to know here.

• Calculating regular deriviatives

• Logarithmic differentiation

• Implicit differentiation

• Deriviative of inverse functions

Related Rates

Know how to solve the following related rates problems:

• Expanding Volumes

• Ladder Problem

• Cylindrical Tank

• Sailing Ships

Q2: A 5m ladder leaning against a wall is pushed towards the wall at a rate of 4 m/s. At what rate is the ladder going up the wall when the base of the ladder is 2 m from the wall?

Show Solution

Let x be the distance from the bottom of the ladder to the wall.

Let y be the distance from the top of the ladder to the floor.

Let t be the time in seconds.

Using the Pythagorean Theorem, we have \(x^2 + y^2 = 5^2\), and implicitly differentiating this gives us.

\[\begin{split}\begin{aligned} \frac{d}{dt} x^2 + y^2 &= \frac{d}{dt} 5^2 \\ 2x\frac{dx}{dt} + 2y\frac{dy}{dt} &= 0 \\ \end{aligned}\end{split}\]

When the ladder is 2 m away from the wall, x = 2. This gives us \(2^2 + y^2 = 25 \Rightarrow y = \sqrt{21}\).

And we know that the ladder is pushed towards the wall at 4 m/s, so \(\frac{dx}{dt} = 4\).

Using this information, we get \(2(2)(4) + 2(\sqrt{21})\frac{dy}{dt} = 0 \Rightarrow \frac{dy}{dt} = \frac{8}{\sqrt{21}}\).

Maximums and Minimums within Intervals

Using the test for absolute extrema as well as the other tests that look at the first and second deriviative, you should be able to find the max and min values of a function given an interval (that can be either open or closed).

Curve Sketching

Know how to sketch a function while also showing all the steps required for curve sketching.

Slope of Tangent Lines

Possible questions that may appear here are:

• Find the tangent line of a function that passes through a point (that may not be on the function)

• Given a line, find the point on a function where that line is the tangent line.

Q3: Find the equations of the lines tangent to \(f(x) = x^2 + 5x + 1\) and passes through the point \((2, 6)\).

Show Solution

One shortcut here is to know the point slope form equation of a line, that is

\(y = m(x - x_0) + y_0\), where \((x_0, y_0)\) is a point on the line.

With this form, you can easily get the equation of a line by substituting \(m\), \(x_0\), and \(y_0\).