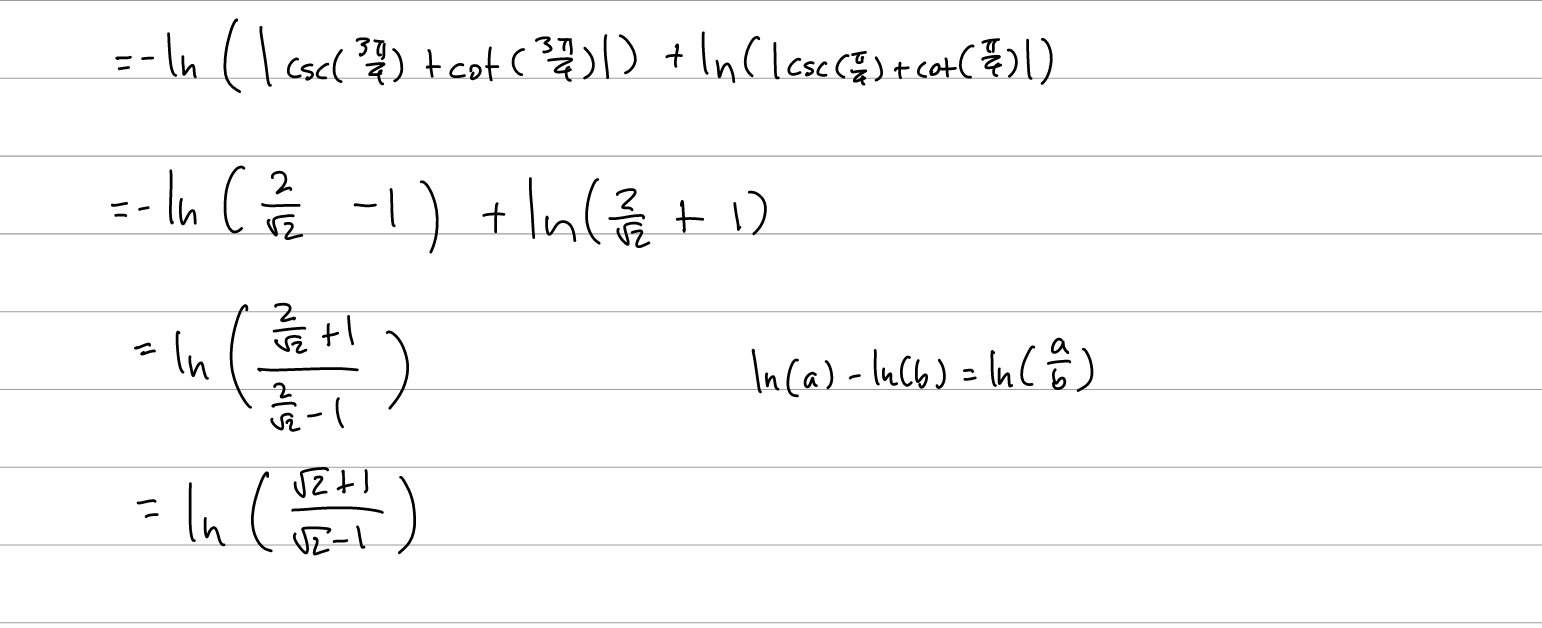Tutorial Week 7
Arc Length
The formula to find the arc length of a function is \(\int_a^b \sqrt{a + (f'(x))^2} \; dx\).
Q1: Find the length of the curve \(y = -ln(sin(x))\) on \(x \in [\frac{\pi}{4}, \frac{3\pi}{4}]\).
Complex Numbers
Complex numbers gives us a way of working with the roots of negative numbers.
The key concepts are:
\(i = \sqrt{-1}\)
Standard form is \(z = a + ib\), where a and b are real numbers
Polar form is represented as \(z = re^{i\theta}\), where r and \(\theta\) are real numbers
Euler’s Formula gives us \(e^{i\theta} = cos\theta + isin\theta\)
Q2: Write \((1 + \frac{2i}{1 - i})^{25}\) in standard form.
\[\begin{split}\begin{aligned}
1 + \frac{2i}{1-i} &= 1 + \frac{2i(i+1)}{(i-1)(i+1)} \\
&= 1 + \frac{2i^2 + 2i}{1 - i^2} \\
&= 1 + \frac{2i - 2}{1 - (-1)} \\
&= 1 + \frac{2i - 2}{2} \\
&= 1 + -1 + i \\
&= i
\end{aligned}\end{split}\]
\[\begin{split}\begin{aligned}
(i)^25 &= i(i^2)^23 \\
&= i(-1)^23 \\
&= i(-1) \\
&= -i
\end{aligned}\end{split}\]
Q3: Write \(z = 2\sqrt{3}e^{\frac{\pi i}{3}}\) in standard form.
We’re given the polar form of a complex number, that is, in the form of \(z = re^{i\theta}\).
So \(r = 2\sqrt{3}\) and \(\theta = -\frac{\pi}{3}\).
Euler’s formula gives us \(e^{i\theta} = cos\theta + isin\theta\).
It follows that:
\[\begin{split}\begin{aligned}
z &= re^{i\theta} \\
&= 2\sqrt{3}e^{i\frac{-\pi}{3}} \\
&= 2\sqrt{3}(cos(-\frac{\pi}{3}) + isin(-\frac{\pi}{3})) \\
&= 2\sqrt{3}(\frac{1}{2} + i(-\frac{\sqrt{3}}{2})) \\
&= \sqrt{3} - 3i
\end{aligned}\end{split}\]