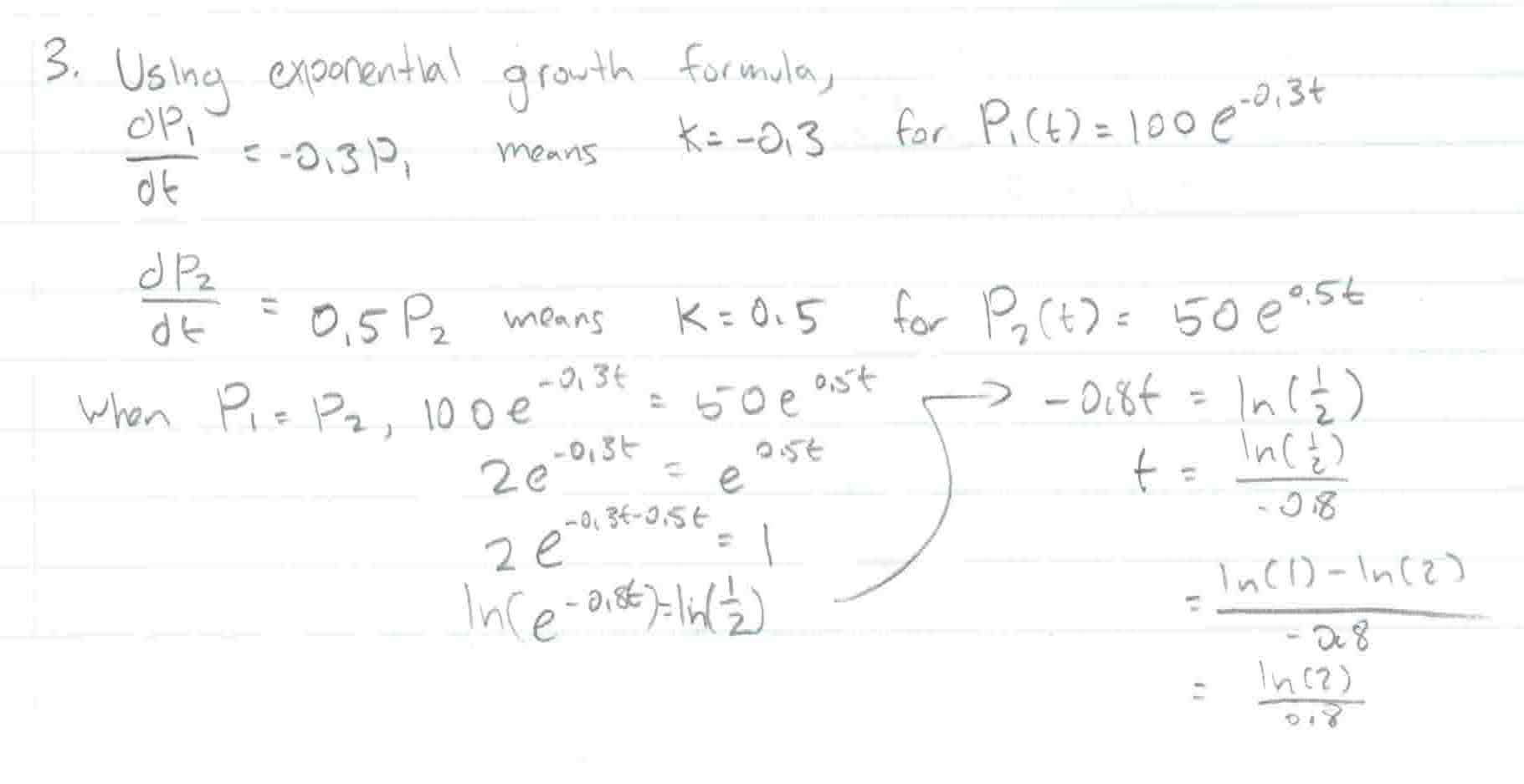Tutorial Week 10

Initial Value Problems

Initial value problems are modelled around the differential equation \(\frac{dy}{dt} = ky\).

If we’re given that equation, and we know \(y(0) = y_0\), then the solution to the differential equation is \(y(t) = y_0e^{kt}\).

You can think of it as \(\frac{dy}{dt} = ky \Rightarrow y(t) = y(0)e^{kt} = y_0e^{kt}\).

Q1: A cell culture starts off with 100 cells and has grown to 300 cells after an hour. Find a formula for the population after t hours (assuming the growth rate is proportional to the size).

Since the growth is proportional to its size, we can model this using the differential equation \(\frac{dy}{dt} = ky\), giving us \(y(t) = y_0e^{kt}\).

We know that \(y(0) = 100\), so now we have the equation \(y(t) = 100e^{kt}\).

We’re given that the population after an hour is 300, meaning \(y(1) = 300\). From the model, we also know that \(y(1) = 100e^{k1} = 100e^k\)

Now, solving for k using \(300 = 100e^k\) gives us:

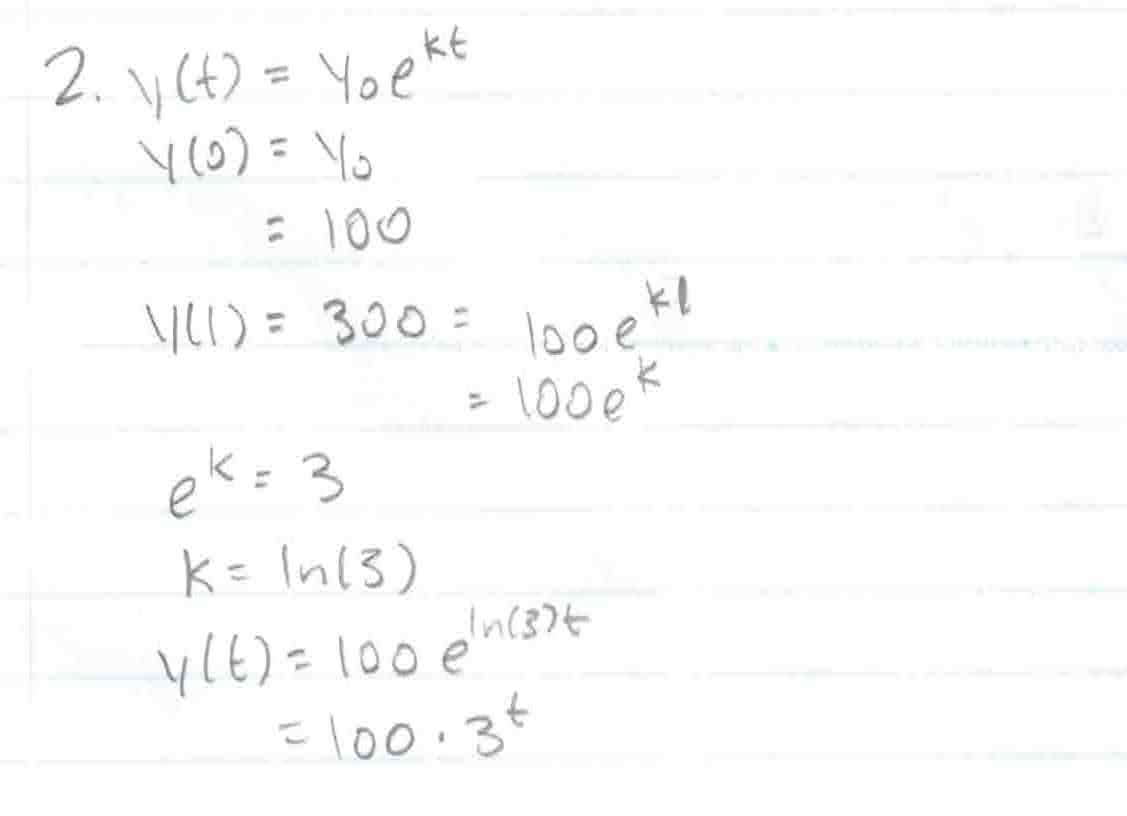
Q2: Let \(P_1\) and \(P_2\) denote the population of two types of bacteria. If \(P_1(0) = 100\), \(P_2(0) = 50\), and \(\frac{dP_1}{dt} = -0.3P_1\) and \(\frac{dP_2}{dt} = 0.5P_2\), when are their populations equal?

Newton’s Law of Cooling

For Newton’s Law of Cooling, we have the formula \(T(t) = T_e + (T_0 - T_e)e^{kt}\), where

\(T(t)\) is the temperature of the object at time t,
\(T_0\) is the initial temperature
\(T_e\) is the environment temperature

Q3: A 60°C object is placed in a 20°C room. After 10 minutes, the temperature of the object is 40°C. What is the temperature of the object after 20 minutes?

Optimization

One method of solving optimization problems is to use the Test for Absolute Extrema, which generally states that:

Given a function \(f(x)\) that is continuous on a closed interval, you can find the absolute maximum and minimum by looking at its critical points and endpoints.

Q4: Find the dimensions of the largest rectangle that fits in between \(x^2\) and \(y=3\).