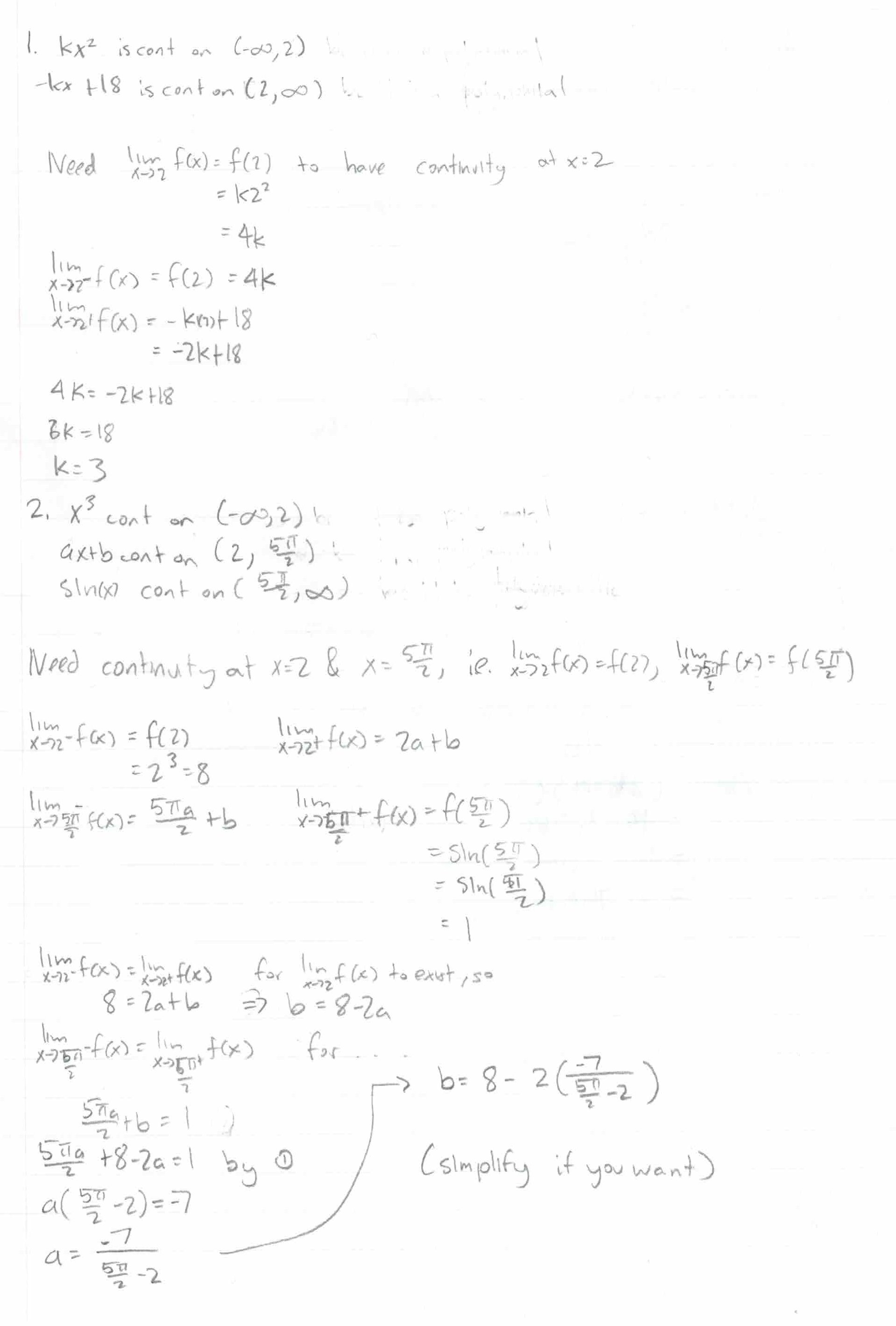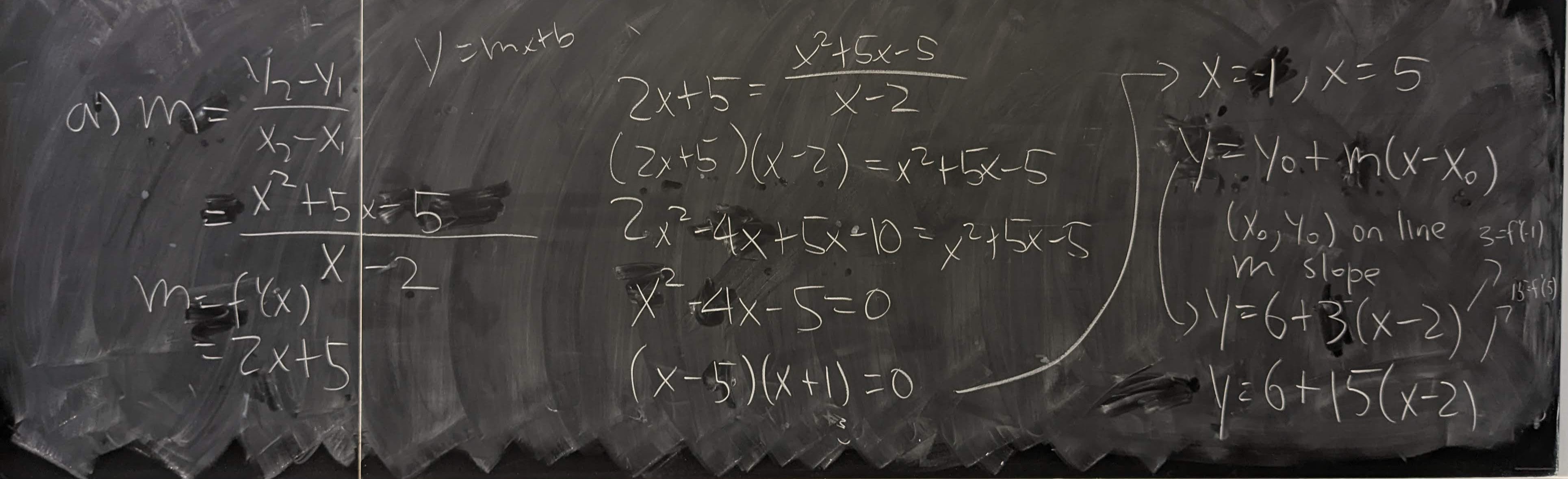Term Test 2 Supplementary Practice

Q1: Definitions

Recalling Definitions

Write down the defintions for the following:

1. Intermediate Value Theorem

2. Extreme Value Theorem

3. Critical Point

4. Inflection Point

5. Continuity at a point

6. Limit definition of a derivative

Show Solution

1. If a function \(f(x)\) is continuous on \([a, b]\) and \(N\) is between \(f(a)\) and \(f(b)\), then there exists a number \(c\) such that \(f(c) = N\).

2. If a function \(f(x)\) is continuous on \([a, b]\), then \(f(x)\) must attain both an absolute maximum and an absolute minimum on \([a, b]\).

3. Point \((c, f(c))\) is a critical point if \(c\) is in the domain of \(f\) and \(f'(c) = 0\) or \(f'(c)\) is undefined.

4. Point \((c, f(c))\) is an inflection point if \(f(x)\) is continuous at \(c\) and the concavity changes at \(c\).

5. A function \(f(x)\) is continuous at \(x = a\) if \(\;lim_{x \to a} f(x) = f(a)\).

6. \(f'(x) = lim_{h \to 0} \frac{f(x + h) - f(x)}{h}\)

Rewriting in the Form of “if … then …”

Some of the statements above can be written in the form of a conditional statement; that is, in the form of “if {condition} then {conclusion}”, e.g. if \(x > 0\) then \(x > -1\).

Fill out the following chart:

Concept	Condition	Conclusion	Full statement: if {condition} then {conclusion}
IVT
EVT
Critical Point
Inflection Point
Continuity at a point

Show Solution

Concept	Condition	Conclusion	Full statement: if {condition} then {conclusion}
IVT	A function \(f(x)\) is continuous on \([a, b]\) and \(N\) is in between \(f(a)\) and \(f(b)\)	There exists a number \(c\) such that \(f(c) = N\)	If a function \(f(x)\) is continuous on \([a, b]\) and \(N\) is in between \(f(a)\) and \(f(b)\) then there exists a number \(c\) such that \(f(c) = N\).
EVT	A function \(f(x)\) is continuous on \([a, b]\)	\(f(x)\) must attain both an absolute maximum and an absolute minimum on \([a, b]\)	If a function \(f(x)\) is continuous on \([a, b]\), then \(f(x)\) must attain both an absolute maximum and an absolute minimum on \([a, b]\).
Critical Point	\(c\) is in the domain of \(f\) and \(f'(c) = 0\) or \(f'(c)\) is undefined	Point \((c, f(c))\) is a critical point	If \(c\) is in the domain of \(f\) and \(f'(c) = 0\) or \(f'(c)\) is undefined then point \((c, f(c))\) is a critical point.
Inflection Point	\(f(x)\) is continuous at \(c\) and the concavity changes at \(c\)	Point \((c, f(c))\) is an inflection point	If \(f(x)\) is continuous at \(c\) and the concavity changes at \(c\) then point \((c, f(c))\) is an inflection point.
Continuity at a point	\(\;lim_{x \to a} f(x) = f(a)\)	\(f(x)\) is continuous at \(x = a\)	If \(\;lim_{x \to a} f(x) = f(a)\) then \(f(x)\) is continuous at \(x = a\).

Q2: Continuity & IVT

Showing that Roots exist

1. Show that \(f\left(x\right)=e^{2x}+2x^{2}-4\) has root in between \(0\) and \(1\).

2. Show that a solution exists for \(2\sin\left(x\right)+1=0\) on the interval \([-\frac{\pi}{2}, \frac{3\pi}{2}]\).

3. Show that \(x^{3}-10x=1\) has at least 3 solutions on the interval \([-4, 4]\).

4. Show that \(f(x)=\pi x^{2}-4\) has two roots in \([-2, 2]\).

Show Sample Solution

Continuity for Piecewise Functions

1. What values of \(k\) makes \(f(x) = \begin{cases} kx^2 & \text{if } x \leq 2 \\ -kx + 18 & \text{if } x \gt 2 \end{cases}\) continuous everywhere.

2. What values of \(a\) and \(b\) make \(f(x) = \begin{cases} x^3 & \text{if } x \leq 2 \\ ax + b & \text{if } 2 \lt x \lt \frac{5\pi}{2} \\ sin(x) & \text{if } x \ge \frac{5\pi}{2} \end{cases}\) continuous everywhere.

3. What values of \(a\) and \(b\) make \(f(x) = \begin{cases} \frac{\left(2ax^{2}+ax+2\right)}{ax-4}& \text{if } x \leq 0 \\ 3ax+b & \text{if } 0 \lt x \lt 1 \\ \frac{\left(bx-6b\right)}{x} & \text{if } x \ge 1 \end{cases}\) continuous everywhere.

Show Solution

Q3: Limit Definition of a Derivative

Applying Limit Definition

Use the limit definition of a derivative for the following (\(f'(x) = lim_{h \to 0} \frac{f(x + h) - f(x)}{h}\)).

1. Find \(f'(x)\) if \(f\left(x\right)=3\sqrt{4x+e}+3x\).

2. Find \(f'(x)\) if \(f\left(x\right)=2x^{2}+4x+3\).

3. Find \(f'(x)\) if \(f\left(x\right)=10x+2\).

4. Find \(f'(x)\) if \(f\left(x\right)=\frac{3}{2x-3}\).

5. Find \(f'(x)\) if \(f\left(x\right)=\frac{7}{\sqrt{x}}\).

6. Find \(f'(x)\) if \(f\left(x\right)=\frac{2}{\sqrt{x+3}}\).

Check your answer by using derivative rules to find the derivative or https://www.derivative-calculator.net/.

Show Hints

1. Split into two limit expressions (one for \(3\sqrt{4x+e}\), the other for \(3x\)). For the former, multiply by the conjugate (\(\frac{\text{conjugate}}{\text{conjugate}}\)).

5. Get a common denominator, then multiply by conjugate.

6. Get a common denominator, then multiply by conjugate.

Q4/5: Computing Derivatives

Directly Computing Derivatives

1. Find \(\frac{df}{dx}\) if \(f\left(x\right)=3x^{3}+\cos\left(x\right)-e^{\sin\left(x\right)}\).

2. Find \(\frac{df}{dx}\) if \(f\left(x\right)=\tan\left(\arctan\left(x\right)+3x^{99}\right)e^{x}\)

3. Find \(\frac{df}{dx}\) if \(f\left(x\right)=5^{\log_4\left(x\right)}+4^{x^{3}}\)

4. Find \(\frac{df}{dx}\) if \(f\left(x\right)=\arcsin\left(x^{2}+x\right)\arctan\left(x^{3}\right)\arccos\left(x\right)\)

4. Find \(\frac{df}{dx}\) if \(f\left(x\right)=\frac{\arctan\left(x\right)-3x^{2}}{2+5xe^{x}}\)

Check your answers using https://www.derivative-calculator.net/.

Derivatives of Inverse Functions

1. Find \((f^{-1})'(x)\) if \(f\left(x\right)=x^{-3}-4\).

2. Find \((f^{-1})'(x)\) if \(f\left(x\right)=6^x\).

3. Find \((f^{-1})'(x)\) if \(f\left(x\right)=ln(x^5)\).

Show Solutions

Logarithmic Differentiation

1. Find \(\frac{df}{dx}\) if \(f\left(x\right)=ex^{ex}\).

2. Find \(\frac{df}{dx}\) if \(f\left(x\right)=\sin\left(x\right)^{\cos\left(x\right)\tan\left(x\right)}\).

3. Find \(\frac{df}{dx}\) if \(f\left(x\right)=f\left(x\right)=\frac{\left(x^{3}+2x+1\right)^{\pi}\left(e^{x}+\cos\left(x\right)\right)^{1142}}{\left(4x+5x^{5}\right)^{3}}\).

Check your answers using https://www.derivative-calculator.net/.

Implicit Differentiation

1. Find \(\frac{dy}{dx}\) for \(3x^{2}y+2xy-y^{3}=0\)

2. Find \(\frac{dy}{dx}\) for \(\arctan\left(x^{3}y\right)=3y\)

3. Find \(\frac{dy}{dx}\) for \(\frac{xy+2}{x^{2}-y}=3y\)

4. Find \(\frac{dy}{dx}\) for \(2^{x^2y^3}=x\)

Check your answers using https://calculator-derivative.com/implicit-differentiation-calculator.

Q6: Related Rates

Formulas to know

Fill out the following table:

Shape	Area/Volume	Perimeter/Surface Area
Triangle		\(\text{Side 1} + \text{Side 2} + \text{Side 3}\)
Rectangle
Right Circular Cylinders
Right Rectangular Prisms

Show Solution

Shape	Area/Volume	Perimeter/Surface Area
Triangle	\(\frac{1}{2}\text{base}\cdot\text{height}\)	\(\text{Side 1} + \text{Side 2} + \text{Side 3}\)
Rectangle	\(\text{length}\cdot\text{width}\)	\(2 \cdot \text{length} + 2 \cdot {width}\)
Right Circular Cylinders	\(\pi \text{r}^2 \text{h}\)	\(2\pi \text{rh} + 2 \pi \text{r}^2\)
Right Rectangular Prisms	\(\text{lwh}\)	\(2\text{lw} + 2\text{wh} + 2\text{lh}\)

Expanding Volumes

1. The radius of a right circular cylinder is growing at a rate of \(2m/s\) while the volume remains the same. How fast is the height changing when the radius is \(1m\)?

2. Suppose you have a right rectangular prism with a width that is increasing at \(3m/s\), height that is increasing at \(5m/s\), and a length that is decreasing at \(1m/s\). How much is the volume changing when the length, width, and height are all \(3m\)?

Sample solution is in practice test 1, question 6.

Ladder Problem

1. A 5m ladder leaning against a wall has its base pushed towards the wall at a rate of \(4m/s\). At what rate was the ladder going up the wall when the base of the ladder was \(2m\) from the wall?

2. An 8m ladder leaning against a wall is sliding down the wall at a rate of \(20m/s\). At what rate was the base sliding away from the wall when the ladder was \(5m\) from the bottom of the wall (height of 5m)?

3. An extendible ladder leaning against a wall is being extended at a rate of \(2m/s\) and is sliding down the wall at a rate of \(1m/s\). How fast was the base of the ladder moving away from the wall when the ladder was \(6m\) from the bottom of the wall?

Sample solution is in practice test 3, question 6.

Cylindrical Tank

1. A cylinder with radius 10m is being filled with a rate of \(3m/s\). How fast is the height changing?

2. The height of water in a cylinder with radius 1m is falling at a rate of \(2m/s\). At what rate does the volume decrease?

Sample solution is in practice test 4, question 6.

Sailing Ships

1. Ship A is 5km north of ship B. Ship A sails west at a rate of \(2km/h\) and ship B sails south at a rate of \(3km/h\). How fast is the distance between the ships changing after three hours?

2. Ship A is 3km south, 5km east of ship B. Ship A sails north at a rate of \(2km/h\) and ship B sails east at a rate of \(1km/h\). How fast is the distance between the ships changing after an hour?

Sample solution is in practice test 2, question 6.

Q7: Absolute Extrema

Test for Absolute Extrema

1. What are the four steps in the test for absolute extrema.

2. Can you use the test for absolute extrema for finding the absolute minimum of \(f(x)=3ln(x)\) in \((3, 10]\)?

3. Find the absolute extrema of \(f(x)=x^2+3-x\) in \([-2, 2]\)

4. Find the absolute extrema of \(f(x)= sin(x)+\frac{x}{\sqrt{2}}\) on the interval \([0, 2\pi]\).

Check your answer using desmos. Your answer should include all the steps of the Test for Absolute Extrema (points might be taken off if you don’t). Refer to practice test 3, question 7 for a sample solution.

Q8: Curve Sketching

Practice Problems

For the below questions, be sure the include all the steps of curve sketching as listed on slide 24 from week 7.

1. Sketch \(f(x) = 2x^3 + x^2 - 4x + 1\).

2. Sketch \(f(x) = x^{6}+x^{2}\).

Check your answer using desmos.

Q9: Tangent Lines

Tangent Line given a Point

1. Find the equations of the lines tangent to \(f(x) = x^2 + 5x + 1\) and passes through the point \((2, 6)\).

2. Find the equation of the line tangent to \(f(x) = \sqrt{x}\) and passes through the point \((-1, 0)\).

Show Tutorial Solution

Point given a Tangent Line

1. Find the point where the line \(y=13x-11\) is the tangent line of \(y=x^{3}+x+5\).

2. Find the point where the line \(y=5x-9\) is the tangent line of \(y=x^{2}-x\).