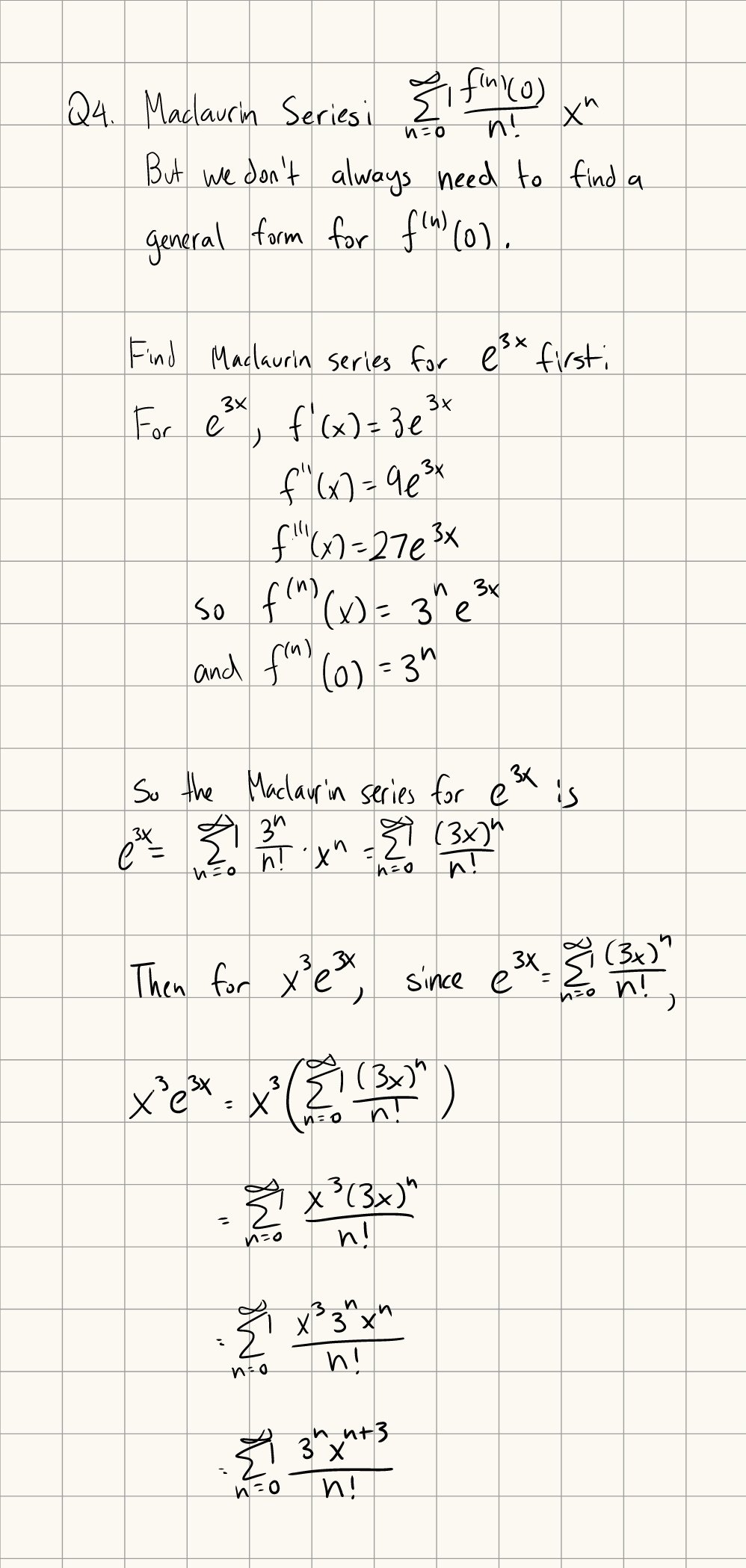Tutorial Week 12

Absolute Convergence

A series \(\sum a_n\) is absolutely convergent if the series \(\sum | a_n |\) converges.

Ratio Test

Given a series \(\sum a_n\),

• If \(\lim_{n \to \infty} | \frac{a_{n+1}}{a_n} | \lt 1\), the series is absolutely convergent

• If \(\lim_{n \to \infty} | \frac{a_{n+1}}{a_n} | \gt 1\), the series diverges

• If \(\lim_{n \to \infty} | \frac{a_{n+1}}{a_n} | = 1\), the ratio test is inconclusive (use another test).

Q1: Use the ratio test to check if \(\sum_{n=1}^\infty \frac{(-5)^n}{(n!)^2}\) converges.

Show Solution

Root Test

Given a series \(\sum a_n\),

• If \(\lim_{n \to \infty} \sqrt[n]{|a_n|} \lt 1\), the series is absolutely convergent

• If \(\lim_{n \to \infty} \sqrt[n]{|a_n|} \gt 1\), the series diverges

• If \(\lim_{n \to \infty} \sqrt[n]{|a_n|} = 1\), the ratio test is inconclusive (use another test).

Q2: Use the root test to check if \(\sum_{n=1}^\infty (\frac{4 + n + ln(n)}{n^2})^n\) converges.

Show Solution

Taylor Series

The Taylor series provides an approximation of a function around some x value in the form of an infinite sum.

The Taylor series of a function \(f(x)\) around \(x = a\) given by the formula \(f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n\).

The Maclaurin Series is a Taylor series around the point \(x = 0\).

Q3: Find the Taylor series for \(f(x) = e^x\) at \(x = 2\).

Show Solution

Q4: Find the Maclaurin series for \(f(x) = x^3e^{3x}\).

Show Solution