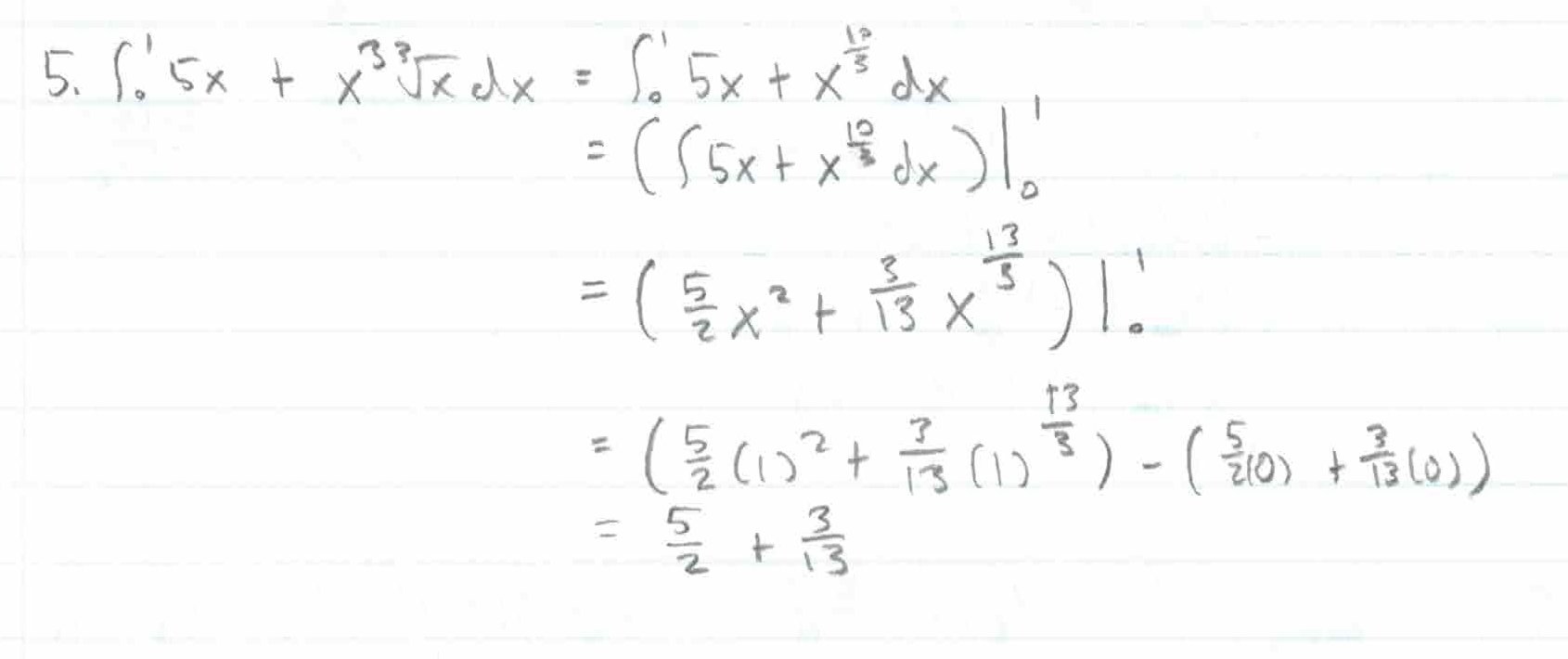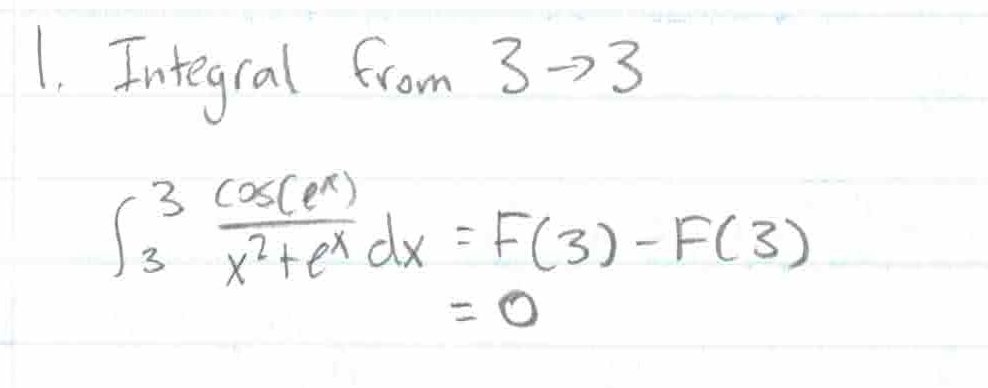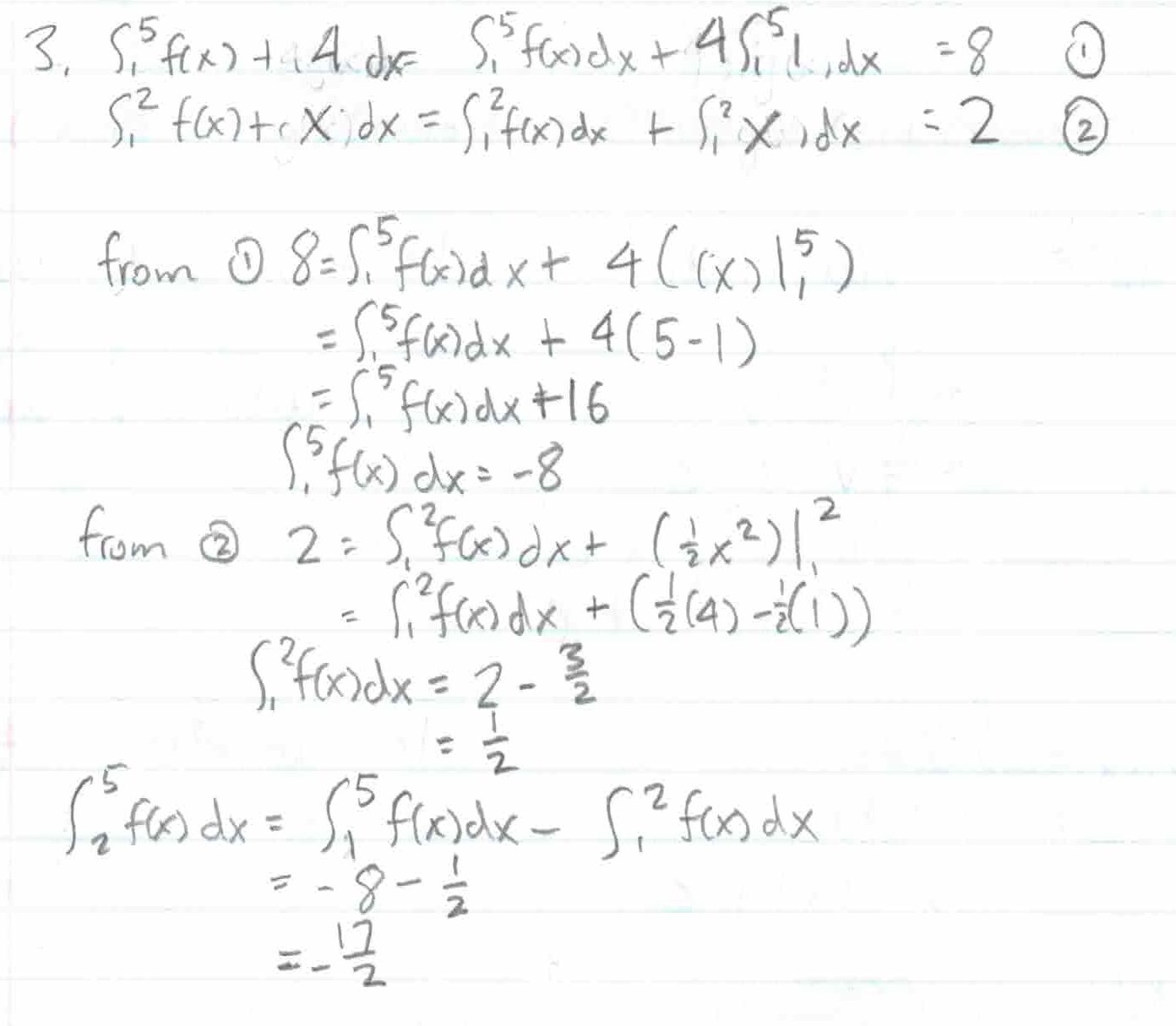Tutorial Week 12
Sigma Notation
We use sigma (\(\Sigma\)) notation as a way to express sums of numbers.
With \(\Sigma_{n=3}^5n^2\), we sum from \(n = 3\) to \(n = 5\) inclusive, giving \(\Sigma_{n=3}^5n^2 = 3^2 + 4^2 + 5^2\).
With sums, we also have a few useful formulas, those being:
\(\Sigma_{k = m}^n ca_k = c\Sigma_{k = m}^n a_k\)
\(\Sigma_{k = m}^n a_k + b_k = \Sigma_{k = m}^n a_k + \Sigma_{k = m}^n b_k\)
\(\Sigma_{k = 1}^n 1 = n\)
\(\Sigma_{k = 1}^n n = \frac{n(n+1)}{2}\)
\(\Sigma_{k = 1}^n n^2 = \frac{n(n+1)(2n+1)}{6}\)
\(\Sigma_{k = 1}^n n^3 = \frac{n^2(n + 1)^2}{4}\)
Riemann Sums
Riemann sums are used to approximate the area under a function by using rectangles.
To define a riemann sum from on the interval [a, b] for f(x), we need:
\(\Delta x = \frac{b - a}{n}\)
\(x_k = a + k\Delta x\) for \(k = 0, 1, 2, ... , n\)
\(x^\ast_k\) is a point in \([x_{k-1}, x_k]\)
The riemann sum is \(\Sigma_{k=1}^n f(x_n^\ast)\Delta x\).
We have two common types of riemann sums, those being the left riemann sum and the right riemann sum.
The left riemann sum is defined with \(x^\ast_k = x_{k-1}\) \(L_n = \Sigma_{k=1}^n f(x_{k-1})\Delta x = \Sigma_{k=1}^n f(a + (k-1)\Delta x)\Delta x\)
The right riemann sum is defined with \(x^\ast_k = x_{k}\) \(R_n = \Sigma_{k=1}^n f(x_{k})\Delta x = \Sigma_{k=1}^n f(a + k\Delta x)\Delta x\)
Q1: Approximate the area under \(10 - x^2\) for \(x \in [0, 1]\) using the right Riemann sum over four intervals.
We first need to find the following:
\(\Delta x = \frac{b - a}{n} = \frac{1 - 0}{4} = \frac{1}{4}\)
\(x_k = a + k\Delta x = 0 + \frac{k}{4}\) for \(k = 0, 1, 2, ... , n\)
\(x^\ast_k = x_{k} = \frac{k}{4}\) since we’re using the right Riemann sum.
\(\Sigma_{k=1}^n f(x_{k})\Delta x = \Sigma_{k=1}^n f(\frac{k}{4})\Delta x\)
Then the right riemann sum is
\(R_n = \Sigma_{k=1}^n f(\frac{k}{4})\Delta x = (\frac{1}{4})((10 - (\frac{1}{4})^2) + (10 - (\frac{2}{4})^2) + (10 - (\frac{3}{4})^2) + (10 - 1^2))\)
Integrals
Integrals are essentially riemann sums with an infinite number of partitions. That is, \(\int_a^b f(x) dx = \lim_{n\to \infty} \Sigma_{k=1}^n f(x^\ast_k) \Delta x\) for the riemann sum over \(x \in [a, b]\). The \(dx\) tells you which variable to integrate, which is useful in multivariable calculus.
Q2: Evaluate \(\int_0^4 2x^2 + x \,dx\) using Riemann sums.
For simplicity, let’s use the right riemann sum.
We have:
\(\Delta x = \frac{b - a}{n} = \frac{4 - 0}{n} = \frac{4}{n}\)
\(x_k = a + k\Delta x = 0 + \frac{4k}{n}\) for \(k = 0, 1, 2, ... , n\)
\(x^\ast_k = x_{k} = \frac{4k}{n}\) since we’re using the right Riemann sum.
So then
Solving for this gives us
Integral Properties and Formulas
\(\int x^n dx = \frac{x^{n+1}}{n+1} + C\) if \(n \neq -1\)
\(\int \frac{1}{x} dx = ln|x| + C\)
\(\int e^x dx = e^x + C\)
(and a few more for trigonometric functions)
\(\int_a^b f(x) + g(x) dx= \int_a^b f(x) dx+ \int_a^b g(x) dx\)
\(\int_a^b kf(x) dx = k \int_a^b f(x) dx\)
\(\int_a^a f(x) dx = 0\)
\(\int_b^a f(x) dx = -\int_a^b f(x) dx\)
\(\int_a^b f(x) dx + \int_b^c f(x) dx = \int_a^c f(x) dx\)
Fundamental Theorem of Calculus 2 (FTC 2)
With FTC 2, you’re able to evaluate integrals at the endpoints of your interval.
If \(\int f(x) dx = F(x)\), then \(\int_a^b f(x) dx = F(x) |_a^b = F(b) - F(a)\)